题目内容
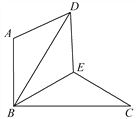
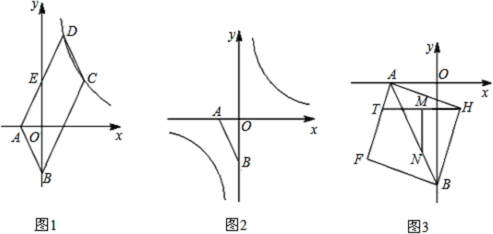
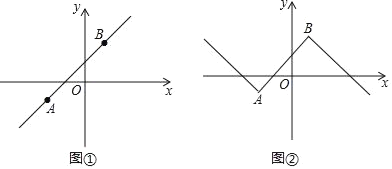
【题目】已知:在平面直角坐标系xOy中,点A(x1,y1)、B(x2,y2)是某函数图象上任意两点(x1<x2),将函数图象中x<x1的部分沿直线y=y1作轴对称,x>x2的部分沿直线y=y2作轴对称,与原函数图象中x1≤x≤x2的部分组成了一个新函数的图象,称这个新函数为原函数关于点A、B的“双对称函数”.例如:如图①,点A(﹣2,﹣1)、B(1,2)是一次函数y=x+1图象上的两个点,则函数y=x+1关于点A、B的“双对称函数”的图象如图②所示.
(1)点A(t,y1)、B(t+3,y2)是函数y=![]() 图象上的两点,y=
图象上的两点,y=![]() 关于点A、B的“双对称函数”的图象记作G,若G是中心对称图形,直接写出t的值.
关于点A、B的“双对称函数”的图象记作G,若G是中心对称图形,直接写出t的值.
(2)点P(![]() ,y1),Q(
,y1),Q(![]() +t,y2)是二次函数y=(x﹣t)2+2t图象上的两点,该二次函数关于点P、Q的“双对称函数”记作f.
+t,y2)是二次函数y=(x﹣t)2+2t图象上的两点,该二次函数关于点P、Q的“双对称函数”记作f.
①求P、Q两点的坐标(用含t的代数式表示).
②当t=﹣2时,求出函数f的解析式;
③若﹣1≤x≤1时,函数f的最小值为ymin,求﹣2≤ymin≤﹣1时,t的取值范围.
【答案】(1)t=![]() ;(2)①P(
;(2)①P(![]() ,t2+t+
,t2+t+![]() ),Q(
),Q(![]() +t,2t+
+t,2t+![]() );②y=
);②y=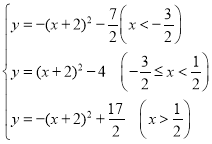 ;③﹣
;③﹣![]() ≤t≤
≤t≤![]() 或
或![]() ≤t≤
≤t≤![]()
【解析】
(1)根据定义、反比例函数图象性质和中心对称性质即可求出t;
(2)①直接代入计算即可;②新函数是分段函数,自变量x的范围分为x<![]() 或
或![]() ≤x≤
≤x≤![]() 或x>
或x>![]() ,二次函数图象翻折后开口方向与原来相反,顶点与原来顶点关于对称轴对称,可以先求新顶点;③分t≤-1,-1<t<0,t≥0进行讨论.
,二次函数图象翻折后开口方向与原来相反,顶点与原来顶点关于对称轴对称,可以先求新顶点;③分t≤-1,-1<t<0,t≥0进行讨论.
解:(1)如图1,

设点A(t,![]() ),A′(t+3,
),A′(t+3,![]() ),
),
∵G是中心对称图形,由反比例函数图象的中心对称性质可知:A与A′关于原点成中心对称,
∴t+t+3=0,解得:t=![]() ;
;
(2)①y1=![]() +2t=t2+t+
+2t=t2+t+![]() ,y2=
,y2=![]() +2t=2t+
+2t=2t+![]()
∴P(![]() ,t2+t+
,t2+t+![]() ),Q(
),Q(![]() +t,2t+
+t,2t+![]() ),
),
②当t=﹣2时,y=(x+2)2﹣4,P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),根据“双对称函数”定义可知:
),根据“双对称函数”定义可知:
新图象f由x<![]() 时抛物线y=(x+2)2﹣4沿直线y=
时抛物线y=(x+2)2﹣4沿直线y=![]() 翻折所得图象、x>
翻折所得图象、x>![]() 时抛物线y=(x+2)2﹣4沿直线y=
时抛物线y=(x+2)2﹣4沿直线y=![]() 翻折所得图象及
翻折所得图象及![]() ≤x≤
≤x≤![]() 时抛物线y=(x+2)2﹣4三个部分组成,
时抛物线y=(x+2)2﹣4三个部分组成,
∴当t=﹣2时,函数f的解析式为:y=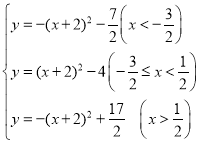
③∵当﹣1≤x≤1时,函数f的最小值为ymin,且﹣2≤ymin≤﹣1,
若t<0,该二次函数关于点P、Q的“双对称函数”为:y=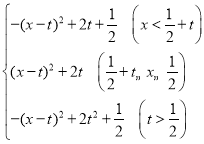 ,
,
当t≤﹣1时,点Q始终是“双对称函数”在﹣1≤x≤1的最低点,由﹣2≤2t+![]() ≤﹣1,∴
≤﹣1,∴![]() ≤t≤
≤t≤![]() ,故
,故![]() ≤t≤﹣1
≤t≤﹣1
当﹣1<t<0时,将x=﹣1代入得y=﹣(﹣1﹣t)2+2t+![]() =﹣t2
=﹣t2![]() ,由﹣2≤﹣t2
,由﹣2≤﹣t2![]() ≤﹣1,解得:
≤﹣1,解得:![]() ≤t≤
≤t≤![]() ,∴﹣1≤t≤
,∴﹣1≤t≤![]()
当t≥0时,由﹣2≤﹣(﹣1﹣t)2+2t2+![]() ≤﹣1,可解得:
≤﹣1,可解得:![]() ≤t≤
≤t≤![]() ,
,
综上所述,t的取值范围为:﹣![]() ≤t≤
≤t≤![]() 或
或![]() ≤t≤
≤t≤![]() ,
,