Question

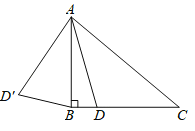
【题目】如图，在Rt△ABC中，∠ABC＝90°，∠C＝30°，点D是线段BC上的动点，将线段AD绕点A顺时针旋转60°至AD'，连接BD'．若AB＝2cm，则BD'的最小值为_____．

Answer 1

【答案】1．

【解析】

在AC上截取AE＝AB＝2，作EF⊥BC于F，如图，先计算出AC＝2AB＝4，BC＝2，∠BAC＝60°，则CE＝2，再在Rt△CEF中计算出EF＝1，FC＝，接着证明△ABD′≌△ADE得到DE＝BE′，然后利用勾股定理得到DE2＝DF2+EF2＝（BD﹣）2+1，然后根据二次函数的性质解决问题．

解：在AC上截取AE＝AB＝2，作EF⊥BC于F，如图，

∵∠ABC＝90°，∠C＝30°，

∴AC＝2AB＝4，BC＝AB＝2，∠BAC＝60°，

∴CE＝AC﹣AE＝2，

在Rt△CEF中，EF＝CE＝1，FC＝EF＝，

∵线段AD绕点A顺时针旋转60°至AD'，

∴AD＝AD′，∠DAD′＝60°，

∴∠BAD′＝∠EAD，

在△ABD′和△ADE中

，

∴△ABD′≌△ADE，

∴DE＝BE′，

在Rt△DEF中，DE2＝DF2+EF2＝（﹣BD）2+12＝（BD﹣）2+1，

∴当BD＝时，DE2有最小值1，

∴BD'的最小值为1．