题目内容
1.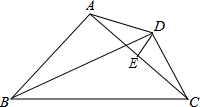 如图,点E为AC的中点,点D为△ABC外一点,且满足射线BD为∠ABC的平分线,∠ABC+∠ADC=180°,请判断DE和AC的位置关系,并证明.
如图,点E为AC的中点,点D为△ABC外一点,且满足射线BD为∠ABC的平分线,∠ABC+∠ADC=180°,请判断DE和AC的位置关系,并证明.
分析 根据∠ABC+∠ADC=180°,所以A,B,C,D四点共圆,得到∠ABD=∠ACD,∠DBC=∠DAC,由射线BD为∠ABC的平分线,得到∠ABD=∠CBD,从而得到∠DAC=∠DCA,即△ADC为等腰三角形,根据等腰三角形的三线合一,即可解答.
解答 解:∵∠ABC+∠ADC=180°,
∴∠BAC+∠BCD=180°,
∴A,B,C,D四点共圆,
∴∠ABD=∠ACD,∠DBC=∠DAC,
∵射线BD为∠ABC的平分线,
∴∠ABD=∠CBD,
∴∠DAC=∠DCA,
∴△ADC为等腰三角形,
∵点E为AC的中点,
∴DE⊥AC(三线合一).
点评 本题考查了四点共圆、等腰三角形的性质,解决本题的关键是证明△ADC为等腰三角形.

练习册系列答案
相关题目
11.已知x2+mx+196是完全平方式,则常数m等于( )
| A. | 28 | B. | -28 | C. | ±28 | D. | ±14 |
13.某个几何体是由一些相同的小正方体构成的,其中三视图如图所示:构成这个几何体的小正方体的个数有( )


| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
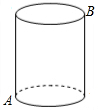 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是多少.
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是多少.