题目内容
如图，∠ACB=∠ADC=90°，BC=a，AC=b，AB=c，要使△ABC与△CAD相似，可取CD等于
- A.
- B.
- C.
- D.
C
分析：本题主要应用两三角形相似，三边对应成比例，解答即可，解题时应对直角三角形中直角边的对应情况进行讨论．
解答：①当△ABC∽△CAD时，
则
，
即：CD=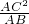
=
，
所以要使△ABC∽△CAD，只要CD等于，
当②△ABC∽△ADC时，
则
，
即：
，
解得：CD=
，
所以要使△ABC∽△ADC，只要CD等于
，
综上可知：CD=或，
故选C．
点评：此题主要考查相似三角形的性质：对应边的比值相等，解题时注意直角三角形的两直角边对应不唯一．
分析：本题主要应用两三角形相似，三边对应成比例，解答即可，解题时应对直角三角形中直角边的对应情况进行讨论．
解答：①当△ABC∽△CAD时，
则
，即：CD=
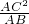=，所以要使△ABC∽△CAD，只要CD等于
，当②△ABC∽△ADC时，
则
，即：
，解得：CD=
，所以要使△ABC∽△ADC，只要CD等于
，综上可知：CD=
或，故选C．
点评：此题主要考查相似三角形的性质：对应边的比值相等，解题时注意直角三角形的两直角边对应不唯一．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
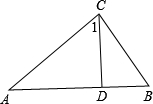如图，△ACB中，∠ACB=90°，∠1=∠B．
13、如图，∠ACB=90°，把Rt△ABC绕点A逆时针旋转90°得到Rt△AB1C1，若BC=1，AB=2，则∠CAB1的度数是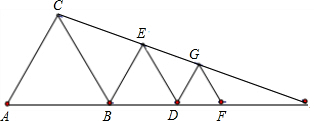
如图，△ACB、△BDE和△DGF都是等边三角形，且点E、G在△ABC边AB的延长线上，设等边的面积分别为S1、S2、S3，若S1=9，S3=1，则S2=
如图，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于D，AD=5cm，DE=2.3cm，则BE的长为
已知：如图，∠ACB=∠DBC，根据图形条件，若增加一个条件