Question

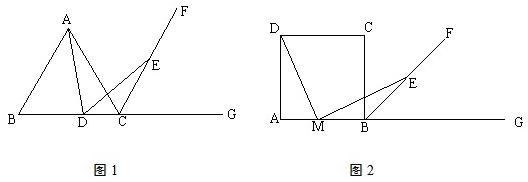
如图1，△ABC是等边三角形，D点是AC的中点，点E在BC的延长线上，且BD=DE．
（1）求证：AD=CE；
（2）若点D不是AC的中点，其他条件不变，如图2，（1）中的结论是否依然成立？若成立请给予证明；若不成立，请说明理由．

Answer 1

（1）证明：∵△ABC是等边三角形，
∴∠ABC=∠CB=60°，AB=AC=BC，
∵D为AC中点，
∴∠DBC=30°，AD=DC，
∵BD=DE，
∴∠E=∠DBC=30°
∵∠ACB=∠E+∠CDE，
∴∠CDE=30°=∠E，
∴CD=CE，
∵AD=DC，
∴AD=CE；

（2）成立，
证明：过D作DF∥BC，交AB于F，
则∠ADF=∠ACB=60°，
∵∠A=60°，
∴△AFD是等边三角形，
∴AD=DF=AF，∠AFD=60°，
∴∠BFD=∠DCE=180°-60°=120°，
∵DF∥BC，
∴∠FDB=∠DBE=∠E，
在△BFD和△DCE中

∴△BFD≌△DCE，
∴CE=DF=AD，
即AD=CE．
分析：（1）求出∠E=∠CDE，推出CD=CE，根据等腰三角形性质求出AD=DC，即可得出答案；
（2）过D作DF∥BC，交AB于F，证△BFD≌△DCE，推出DF=CE，证△ADF是等边三角形，推出AD=DF，即可得出答案．
点评：本题考查了全等三角形性质和判定，等边三角形性质的应用，题目比较典型，是一道比较好的题目．