Question

【题目】阅读下面材料：

在数学课上，老师提出利用尺规作图完成下面问题：

已知：△OAB.

求作：⊙O，使⊙O与△OAB的边AB相切.

小明的作法如下：

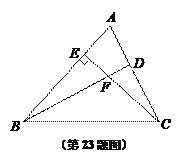
如图，①取线段OB的中点M；以M为圆心，MO为半径作⊙M，与边AB交于点C；

②以O为圆心，OC为半径作⊙O；

所以，⊙O就是所求作的圆.

请回答：这样做的依据是__________________________________________________．

Answer 1

【答案】圆的定义，直径的定义，直径所对的圆周角为90°，到线段两端点距离相等的点在线段的垂直平分线上，经过半径的外端并且垂直于这条半径的直线是圆的切线.

【解析】∵要作出线段OB的中点M，

∴需作线段OB的垂直平分线，交OB于点M，

∴OM=MB（线段垂直平分线上的点到线段两端的距离相等）；

∵以M为圆心，MO为半径作⊙M（圆的定义），

∴OB是⊙M的直径（直径定义），

∴∠OCB=90°（直径所对的圆周角是直角），

又∵是以O为圆心，OC为半径作的⊙O（圆的定义），

∴AB经过OC，且AB⊥OC，

∴AB是⊙O的切线（经过半径的外端，并垂直于这条半径的直线是圆的切线）.

综上可知：本题的作图依据是：圆的定义，直径的定义，直径所对的圆周角为90°，到线段两端点距离相等的点在线段的垂直平分线上，经过半径的外端并且垂直于这条半径的直线是圆的切线.