Question

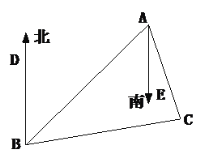
【题目】如图，在直角三角形中，,点是的内心，的延长线和三角形的外接圆相交于点，连结.

（1）求证：；

（2）过点作的平行线交、的延长线分别于点、，已知，圆的直径为，

①求证：为圆的切线；②求的长.

Answer 1

【答案】（1）证明见解析；（2）①证明见解析；②

【解析】

（1）先判断出∠DAC＝∠DAB，∠ABH＝∠CBH，进而判断出∠DHB＝∠DBH，即可得出结论；

（2））①先判断出OD∥AC，进而判断出OD⊥EF，即可得出结论；

②先判断出△CDE≌△BDG，得出GB＝CE＝1，再判断出△DBG∽△ABD，求出DB2＝5，即DB＝，DG＝2，进而求出AE＝AG＝4，最后判断出△OFD∽△AFE即可得出结论．

（1）连结,

∵点为的内心，

∴,,

而，

,

又∵，

，

∴.

（2）①连结，

∵.

∴∥.

∵,∥.

∴，

∴.

∴是圆的切线；

②如图，过点作于点，

∵，

∴，，，

∴≌，

∴.

在中，，

∴，又，

∴∽,

∴.

∴，，∴

又∵为内心，∴，

而∥ ∴∽.

∴.

即 ∴.