题目内容
如图,在正方形网格上,每个小正方形的边长为a,那么△ABC与△A1B1C1是否相似?为什么?
【答案】分析:根据勾股定理分别计算△ABC与△A1B1C1三边长,根据三角形三边的比值相等可以证明三角形相似,即可解题.
解答:证明:∵每个小正方形的边长为a,
AB= a,AC=
a,AC= a,BC=5a,A1B1=
a,BC=5a,A1B1= a,A1C1=2a,B1C1=
a,A1C1=2a,B1C1= a
a

∴△ABC∽△A1B1C1.
点评:本题考查了勾股定理在直角三角形中的运用,考查了相似三角形的证明和相似三角形对应边比值相等的性质,本题中分别求△ABC与△A1B1C1的三边长是解题的关键.
解答:证明:∵每个小正方形的边长为a,
AB=
 a,AC=
a,AC= a,BC=5a,A1B1=
a,BC=5a,A1B1= a,A1C1=2a,B1C1=
a,A1C1=2a,B1C1= a
a
∴△ABC∽△A1B1C1.
点评:本题考查了勾股定理在直角三角形中的运用,考查了相似三角形的证明和相似三角形对应边比值相等的性质,本题中分别求△ABC与△A1B1C1的三边长是解题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
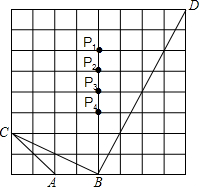 如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.
如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.| A、P1 | B、P2 | C、P3 | D、P4 |
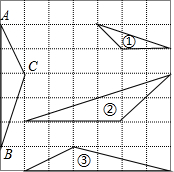 如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有
如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有 如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是
如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是 如图,在正方形网格上有△ABC和△DEF.
如图,在正方形网格上有△ABC和△DEF. 作图计算题.
作图计算题.