题目内容
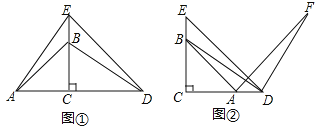
【题目】如图,![]() 中,
中,![]() 和
和![]() 分别平分
分别平分![]() 和
和![]() 的外角
的外角![]() ,一动点
,一动点![]() 在
在![]() 上运动,过点
上运动,过点![]() 作
作![]() 的平行线与
的平行线与![]() 和
和![]() 的角平分线分别交于点
的角平分线分别交于点![]() 和点
和点![]() .
.

![]() 求证:当点
求证:当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 为矩形,说明理由;
为矩形,说明理由;
![]() 在第
在第![]() 题的基础上,当
题的基础上,当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 为正方形,说明理由.
为正方形,说明理由.
【答案】(1)当点![]() 运动到
运动到![]() 的中点位置时,四边形
的中点位置时,四边形![]() 为矩形;理由见解析;(2)当
为矩形;理由见解析;(2)当![]() 时,四边形
时,四边形![]() 为正方形,理由见解析
为正方形,理由见解析
【解析】
(1)利用角平分线的性质以及平行线的性质得出OE=OF,即可得出结论;
(2)证出EF⊥AC,即可得出结论.
![]() 证明:当点
证明:当点![]() 运动到
运动到![]() 的中点位置时,四边形
的中点位置时,四边形![]() 为矩形;理由如下:
为矩形;理由如下:
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理可证,![]() ,
,
∴![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形;
为矩形;
![]() 解:当
解:当![]() 时,四边形
时,四边形![]() 为正方形;
为正方形;
理由如下:∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 为矩形,
为矩形,
∴四边形![]() 为正方形.
为正方形.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案【题目】某校八年级共有300位学生.为了解该年级学生地理、生物两门课程的学习情况,从中随机抽取60位学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理和分析,下面给出了部分信息.
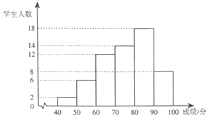
信息1:如图是地理课程成绩的条形统计图 (数据分成6组:第一组40≤![]() <50;第二组50≤
<50;第二组50≤![]() <60;第三组60≤
<60;第三组60≤![]() <70;第四组70≤
<70;第四组70≤![]() <80;第五组80≤
<80;第五组80≤![]() <90;第六组90≤
<90;第六组90≤![]() ≤100):
≤100):
信息2:地理课程测试在第四组70≤![]() <80的成绩是:
<80的成绩是:
70 71 71 71 73 73 75 75 76.5 76.5 78 78 79 79.5
信息3:地理、生物两门课程成绩的平均数、中位数、众数如下表:
课程 | 平均数 | 中位数 | 众数 |
地理 | 73.8 |
| 83.5 |
生物 | 72.2 | 70 | 82 |
根据以上信息,回答下列问题:
(1)所抽取的60位学生地理课程成绩的中位数落在第几组?写出这60位学生地理课程测试成绩的中位数![]() ;
;
(2)在此次测试中,某学生的地理课程成绩为75分,生物课程成绩为71分,该生成绩排名更靠前的课程是地理还是生物?说明理由;
(3)假设该年级学生都参加此次测试,估计地理课程成绩超过73.8分的人数.