题目内容
如图所示,正方形ABCD的边长为4,E为CD 的中点,F为AD边上一点,且不与点D重合,AF=a。
(1)判断四边形BCEF的面积是否存在最大或最小值,若存在,求出最大或最小值;若不存在,请说明理由;
(2)若∠BFE=∠FBC,求tan∠AFB的值;
(3)在(2)的条件下,若将“E为CD的中点”改为“CE=k·DE”,其中k为正整数,其他条件不变,请直接写出tan∠AFB的值。(用k的代数式表示)
(1)判断四边形BCEF的面积是否存在最大或最小值,若存在,求出最大或最小值;若不存在,请说明理由;
(2)若∠BFE=∠FBC,求tan∠AFB的值;
(3)在(2)的条件下,若将“E为CD的中点”改为“CE=k·DE”,其中k为正整数,其他条件不变,请直接写出tan∠AFB的值。(用k的代数式表示)

|
解:(1)如图①, |
 |
| (2)如图②,延长BC、FE交于点P, ∵正方形ABCD中,AD∥BC, ∴△DEF∽△CEP, ∵E为CD的中点,  = = =1,PF=2EF =1,PF=2EF∵∠BFE=∠FBC ∴PB=PF, ∴AF=a, ∴PC=DF=4-a,PB=PF=8-a,EF=  , ,∵Rt△DEF中,EF2=DE2+DF2, ∴(  )2 =22+(4-a)2, )2 =22+(4-a)2,整理,得3a2-16a+16=0, 解得a1=  ,a2=4 ,a2=4∵F点不与D点重合, ∴a=4不成立, ∴a=  ,tan∠AFB= ,tan∠AFB= =3; =3; |
 |
| (3) tan∠AFB=2k+l。(K为正整数) |

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
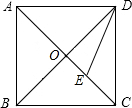 如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )
如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|
 ×4×a×2×(4一a)=12-a,
×4×a×2×(4一a)=12-a,  4、如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
4、如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )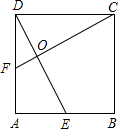 如图所示,正方形ABCD中,E为AB中点,F为AD中点,DE、CF交于O点,求证:DE⊥CF.
如图所示,正方形ABCD中,E为AB中点,F为AD中点,DE、CF交于O点,求证:DE⊥CF. 如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是
如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是 如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: