题目内容
18、如图，一条直线上依次摆放着三个正方形．已知斜着放置的一个正方形的面积为s1，正着放置的两个正方形的面积分别为3、2，则s1=5
．分析：根据题意，可以证得中间的两个三角形全等，再根据勾股定理，即可得出答案．
解答：解：如下图所示：
∵三个四边形均为正方形，
∴∠ACB+∠BAC=90°、∠ACB+∠DCE=90°，AC=CE，
∴∠BAC=∠DCE，
∵∠ABC=∠CDE=90°，
∴△ABC≌△CDE，
∴BC=DE，
∴AC2=AB2+BC2，
∵两个正方形的面积分别为3、2，
∴AC2=5，
即S1=5．
∵三个四边形均为正方形，
∴∠ACB+∠BAC=90°、∠ACB+∠DCE=90°，AC=CE，
∴∠BAC=∠DCE，
∵∠ABC=∠CDE=90°，
∴△ABC≌△CDE，
∴BC=DE，
∴AC2=AB2+BC2，
∵两个正方形的面积分别为3、2，
∴AC2=5，
即S1=5．
点评：本题考查了勾股定理的运用，结合正方形的面积求解公式求解．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
达到C港．设甲、乙两船行驶x（h）后，与B港的距离分别为y1、y2（km），y1、y2与x的函数关系如图所示．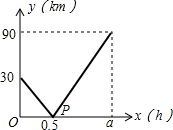
（2013•溧水县一模）在一条直线上依次有A、B、C三个海岛，某海巡船从A岛出发沿直线匀速经B岛驶向C岛，执行海巡任务，最终达到C岛．设该海巡船行驶x（h）后，与B港的距离为y（km），y与x的函数关系如图所示．
如图，一条直线上依次摆放着三个正方形．已知斜着放置的一个正方形的面积为s1，正着放置的两个正方形的面积分别为3、2，则s1=________．