Question

【题目】已知中，点为斜边的中点，连接将沿直线翻折，使点落在点的位置，连接交于点若则的值为（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

直角三角形的勾股定理和斜边中线等于斜边一半可以得到等腰三角形的边长，通过作辅助线，可将所求的问题进行转化求BE，由折叠得CD是BE的中垂线，借助三角形的面积公式，可以求出BG，进而求出BE，由等腰三角形的性质，可得DN是三角形的中位线，得到DN等于BE的一半，求出DN，在根据勾股定理，求出AN，进而求出AE．

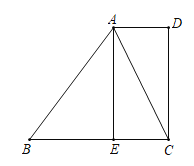
解：过点D作DM⊥BC，DN⊥AE，垂足为M、N，连接BE交CD于点G，

∵Rt△ACB中，AB==10，

∵点D为斜边AB的中点，

∴CD=AD=BD=AB=5，

在△DBC中，DC=DB，DM⊥BC，

∴MB=MC=BC=3，

∴DM==4，

由折叠得，CD垂直平分BE，∠BDC=∠EDC，

在△ADE中，DA=DE，DN⊥AE，

∴AN=NE=AE，

∴DN是△ABE的中位线，

∴DN//BE，DN=BE，

在△DBC中，由三角形的面积公式得：BCDM=DCBG，

即：6×4=5×BG，

∴BG==DN，

在Rt△ADN中，AN=，

∴AE=2AN=，

故选：B．