题目内容
 如图,AB=AC,点E在BC上,点D在AE上,∠BAC=∠BDE=2∠CDE,求证:BE=2CE.
如图,AB=AC,点E在BC上,点D在AE上,∠BAC=∠BDE=2∠CDE,求证:BE=2CE.考点:全等三角形的判定与性质
专题:证明题
分析:在AE上截取AM=BD,连接CM,过点C作CN∥DB,交AE的延长线于点N,易证△CAM≌△ABD,可得∠CMN=∠BDE,即可求得CN=CM,进而可以求得AD=DM=CM=CN,即BD=2CN,根据CN∥DB即可解题.
解答:解:在AE上截取AM=BD,连接CM,过点C作CN∥DB,交AE的延长线于点N.

∵∠BAC=∠BDE,
∴∠BAD+∠CAM=∠BAD+∠ABD,
∴∠CAM=∠ABD,
∵在△CAM和△ABD中,
,
∴△CAM≌△ABD,(SAS)
∴∠CMA=∠ADB,CM=AD,
∴∠CMN=∠BDE,
∵CN∥DB,
∴∠N=∠BDE,
∴∠CMN=∠N,
∴CN=CM,
∵∠BDE=2∠CDE,
∴∠CMN=2∠CDE,
∵∠CMN=∠CDE+∠DCM,
∴∠CDE=∠DCM,
∴DM=CM,
∴AD=DM=CM=CN,
∴AD+DM=2CN,即AM=2CN,
∴BD=2CN,
∵CN∥DB,
∴BE=2EC.

∵∠BAC=∠BDE,
∴∠BAD+∠CAM=∠BAD+∠ABD,
∴∠CAM=∠ABD,
∵在△CAM和△ABD中,
|
∴△CAM≌△ABD,(SAS)
∴∠CMA=∠ADB,CM=AD,
∴∠CMN=∠BDE,
∵CN∥DB,
∴∠N=∠BDE,
∴∠CMN=∠N,
∴CN=CM,
∵∠BDE=2∠CDE,
∴∠CMN=2∠CDE,
∵∠CMN=∠CDE+∠DCM,
∴∠CDE=∠DCM,
∴DM=CM,
∴AD=DM=CM=CN,
∴AD+DM=2CN,即AM=2CN,
∴BD=2CN,
∵CN∥DB,
∴BE=2EC.
点评:本题考查了全等三角形的判定和全等三角形对应角、对应边相等的性质,考查了三角形外角等于不相邻两内角的性质,本题中求证△CAM≌△ABD是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2015年南箐小学的营养餐费用大约用去1370000元,将1370000用科学记数法表示为( )
| A、137×104 |
| B、13.7×105 |
| C、1.37×106 |
| D、1.37×104 |
一个几何体由若干大小相同的小正方形搭成,从正面、上面看到的这个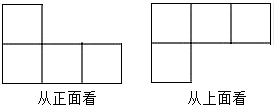 几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )
几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )
 几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )
几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )| A、4个 | B、5个 | C、6个 | D、7个 |
 已知,如图,在四边形ABCD中,BC>AB,∠A+∠C=180°,AD=DC.求证:BD平分∠ABC.
已知,如图,在四边形ABCD中,BC>AB,∠A+∠C=180°,AD=DC.求证:BD平分∠ABC. 如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个.
如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个.