Question

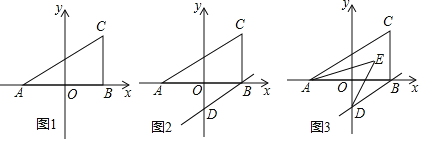
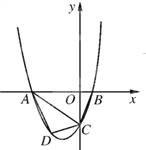
【题目】已知，如图抛物线y＝ax2＋3ax＋c(a>0)与y轴交于点C，与x轴交于A， B两点，点A在点B左侧．点B的坐标为(1,0)，OC＝3OB.

（1）求抛物线的解析式；

（2）若点D是线段AC下方抛物线上的动点，过点D做x轴的垂线，交AC于点E,求线段DE的最大值.

（3）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值.

Answer 1

【答案】（1）y＝x2＋x－3；（2）3；（3）四边形ABCD面积有最大值.

【解析】试题分析：（1）已知了B点坐标，易求得OB、OC的长，进而可将B、C的坐标代入抛物线中，求出待定系数的值，即可得出抛物线的解析式．

（2）根据A、C的坐标，易求得直线AC的解析式．可过D作x轴的垂线，交AC于E，x轴于F；易得△ADC的面积是DE与OA积的一半，可设出F点的坐标，分别代入直线AC和抛物线的解析式中，即可求出DE的长；

（3）由四边形ABCD的面积与F点横坐标间的函数关系式，根据所得函数的性质即可求出四边形ABCD的最大面积；由于AB、OC都是定值，则△ABC的面积不变，若四边形ABCD面积最大，则△ADC的面积最大.

试题解析：（1）∵B(1，0)，

∴OB=1；

∵OC=3BO，

∴C(0,3)；

∵y=ax2+3ax+c过B(1,0)、C(0,3)，

∴；

解这个方程组，得，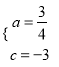

∴抛物线的解析式为：y＝x2＋x－3；

（2）如图：

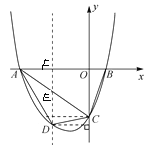
∵A(－4，0)，C(0，－3)，

设直线AC的解析式为y＝kx＋b，

代入求得：y＝－x－3，

令D（x， x2＋x－3），E（x，－ x－3），

则DE＝－x－3－x2＋x－3＝－ (x＋2)2＋3.

∴当x＝－2时，DE有最大值3；

（3）S四边形span>ABCD＝S△ABC＋S△ACD＝＋·DE·(AF＋OF)＝＋2DE，

∴当DE取最大值3时，四边形ABCD面积有最大值.