题目内容
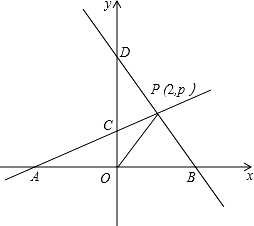
已知,A、B 分别是 x 轴上位于原点左、右两侧的点,点 P 在第一象限,直线 PA 交 y 轴于点 C
(0,2),直线 PB 交 y 轴于点 D,S△AOP=6.
(1)求△COP 的面积; 求点 A 的坐标和 m 的值;
(3)若 S△BOP=S△DOP,求直线 BD 的函数解析式.
【考点】两条直线相交或平行问题.
【专题】代数几何综合题;待定系数法.
【分析】(1)已知 P 的横坐标,即可知道△OCP 的边 OC 上的高长,利用三角形的面积公式即可求 解;
求得△AOC 的面积,即可求得 A 的坐标,利用待定系数法即可求得 AP 的解析式,把 x=2 代入解析 式即可求得 p 的值;
(3)设直线 BD 的解析式为 y=kx+b(a≠0),再把 P 代入得出 2k+b=3,故可得出 D(0,b),B(﹣  ,0),再根据三角形的面积公式即可得出结论.
,0),再根据三角形的面积公式即可得出结论.
【解答】解:(1)作 PE⊥y 轴于 E,
∵P 的横坐标是 2,则 PE=2.
∴S△COP=  OC•PE=
OC•PE=  ×2×2=2;
×2×2=2;
∴S△AOC=S△AOP﹣S△COP=6﹣2=4,
∴S△AOC=  OA•OC=4,即
OA•OC=4,即  ×OA×2=4,
×OA×2=4,
∴OA=4,
∴A 的坐标是(﹣4,0).
设直线 AP 的解析式是 y=kx+b,则
 .
.

练习册系列答案
相关题目
 .
.
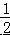 的倒数是
的倒数是