题目内容
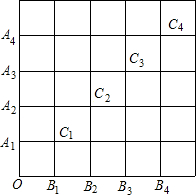 观察右图,大正方形由边长为1的小正方形组成
观察右图,大正方形由边长为1的小正方形组成SOA1C1B1=1,
SOA2C2B2=1+3=4
…
完成填空SOA4C4B4=
你能找到它的规律吗?找到后计算1+3+5+…+1999的值.
分析:正方形的面积和奇数依次相加的规律,根据第一个正方形的面积为1,第二个为1+3=4,第三个为1+3+5=9,第4个为1+3+5+7=16,可求出第n个正方形的面积,从而可求出1+3+5+…+1999的值.
解答:解:SOA4C4B4=1+3+5+7=16.
故答案为:16.
第一个正方形的面积为:1.
第二个正方形的面积为:1+3=4=22.
第三个正方形的面积为:1+3+5=9=32.
第四个正方形的面积为:1+3+5+7=16=42.
第n个正方形的面积为:1+3+5+7+…+(2n-1)=(
)2=n2.
∴1+3+5+…+1999=(
)=(103)2=106.
故答案为:16.
第一个正方形的面积为:1.
第二个正方形的面积为:1+3=4=22.
第三个正方形的面积为:1+3+5=9=32.
第四个正方形的面积为:1+3+5+7=16=42.
第n个正方形的面积为:1+3+5+7+…+(2n-1)=(
| 2n-1+1 |
| 2 |
∴1+3+5+…+1999=(
| 1999+1 |
| 2 |
点评:本题考查的是一个规律性问题,关键看到奇数依次相加,和边长从1开始,依次增加1的正方形的面积的关系,从而求出解.

练习册系列答案
相关题目
 观察右图,大正方形由边长为1的小正方形组成
观察右图,大正方形由边长为1的小正方形组成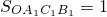 ,
,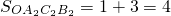
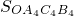 =________
=________