题目内容
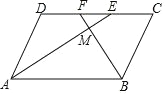
【题目】如图,在一个内角为60°的菱形 ABCD中,AB=2,点P以每秒1cm的速度从点A出发,沿AD→DC的路径运动,到点C停止,过点P 作PQ⊥BD,PQ 与边AD(或边CD)交于点Q,△ABQ的面积y(cm2)与点P 的运动时间x(秒)的函数图象大致是( )

A. B.
B. C.
C.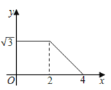 D.
D.
【答案】C
【解析】
由题意根据动点P的运动过程分两种情况说明:①PQ与边CD交于点Q时,过点D作DE⊥AB于点E,根据在边长为2一个内角为60°的菱形ABCD中,即可求当0≤x≤2时,y=![]() ;②当PQ与边AD交于点Q时,过点Q作QE⊥AB于点E,即可求当2<x≤4时,y=-
;②当PQ与边AD交于点Q时,过点Q作QE⊥AB于点E,即可求当2<x≤4时,y=-![]() x+4
x+4![]() ,进而可判断,△ABQ的面积y(cm2)与点P的运动时间x(秒)的函数图象.
,进而可判断,△ABQ的面积y(cm2)与点P的运动时间x(秒)的函数图象.
解:①PQ与边CD交于点Q时,
如图,过点D作DE⊥AB于点E,
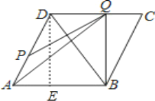
∴∠DEA=90°,
在边长为2一个内角为60°的菱形ABCD中,
AD=DC=2,∠DAB=60°,
∴AE=1,![]() ,
,
∴![]() ,
,
即当0≤x≤2时,![]() .
.
该函数图象是平行于x轴的一段线段;
②当PQ与边AD交于点Q时,如图,过点Q作QE⊥AB于点E,
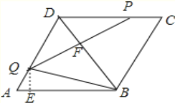
∴∠QEA=90°,
∵PQ⊥BD,
∴∠DFP=∠DFQ=90°,
∵四边形ABCD是菱形,
∴BD平分∠ADC,
∴∠CDB=∠ADB,
DF=DF,
∴△DFP≌△DFQ(ASA),
∴DP=DQ,
∵AD=DC=2,
∴AQ=PC=4-x,
∴在Rt△AQE中,∠QAE=60°,
∴![]() ,
,
∴![]()
即当2<x≤4时,![]() ,
,
该函数图象是y随x的增大而减小的一段线段.
所以△ABQ的面积y(cm2)与点P的运动时间x(秒)的函数图象大致是选项C.
故选:C.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目