题目内容
如果x+
=a,求x6+
的值.
| 1 |
| x |
| 1 |
| x6 |
考点:分式的混合运算,完全平方公式
专题:计算题
分析:把已知等式两边平方,利用完全平方公式化简求出x2+
的值,
| 1 |
| x2 |
解答:解:把已知等式x+
=a两边平方,得:(x+
)2=x2+
+2=a2,即x2+
=a2-2,
∴x4+
=(x2+
)2-2=a4-4a2+4-2=a4-2a2+2,
则原式=(x2+
)(x4+
-1)=(a2-2)(a4-2a2+1)=a6-4a4+5a2-2.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x2 |
∴x4+
| 1 |
| x4 |
| 1 |
| x2 |
则原式=(x2+
| 1 |
| x2 |
| 1 |
| x4 |
点评:此题考查了分式的混合运算,以及完全平方公式的运用,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
下列二项式中,能用平方差公式分解因式的是( )
| A、x2+4y2 |
| B、-4y2+x2 |
| C、-x2-4y2 |
| D、x-4y2 |
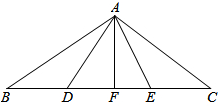 如图,点D,E在△ABC的边BC上,现有3个语句:①AB=AC;②AD=AE;③BD=CE.
如图,点D,E在△ABC的边BC上,现有3个语句:①AB=AC;②AD=AE;③BD=CE.