题目内容
若⊙P与函数图象有且只有一个公共点,并且与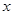 轴、
轴、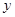 轴都相切的圆,则称⊙P是这个函数的伴圆.
轴都相切的圆,则称⊙P是这个函数的伴圆.
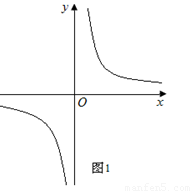
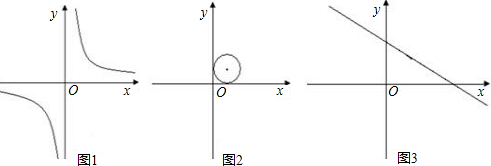
【小题1】如图1,求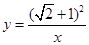 的伴圆的圆心P的坐标及半径r;
的伴圆的圆心P的坐标及半径r;
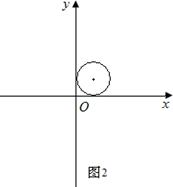
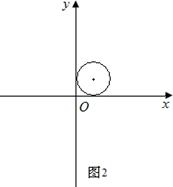
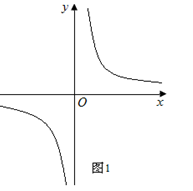
【小题2】如图2,⊙P的半径为1,若⊙P是二次函数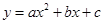 的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;
的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;
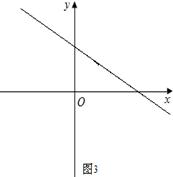
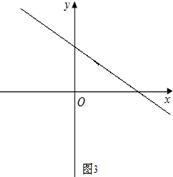
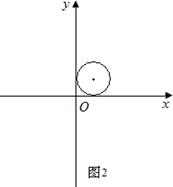
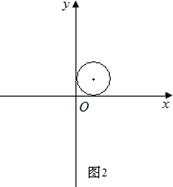
【小题3】如图3,求一次函数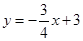 的所有伴圆的圆心P的坐标及半径.
的所有伴圆的圆心P的坐标及半径.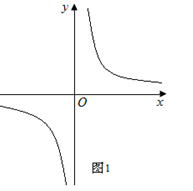
【小题1】在一、三象限内,到x轴、y轴距离相等的点在 上,
上, 与
与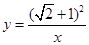 在第一象限的交点坐标
在第一象限的交点坐标 .∴
.∴ ,解得:
,解得: ,
, ,
,
同理伴圆在第三象限时,
【小题2】 ,
, 的伴圆均为⊙P,
的伴圆均为⊙P, ,(a<0);
,(a<0); ,(a>0)的伴圆也都是⊙P.
,(a>0)的伴圆也都是⊙P.
【小题3】∵ 时,
时, ;
; 时,
时, ,
,
∴ .
.
①∵ ,
,
∴ ,解得:
,解得: ,∴
,∴ ;
;
②∵ ,
,
∴ ,解得:
,解得: ,∴
,∴ ;
;
③∵ ,
,
∴ ,解得:
,解得: ,∴
,∴ ;
;
④∵ ,
,
∴ ,解得:
,解得: ,∴
,∴ .
.
解析

练习册系列答案
相关题目
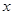 轴、
轴、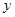 轴都相切的圆,则称⊙P是这个函数的伴圆.
轴都相切的圆,则称⊙P是这个函数的伴圆.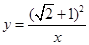 的伴圆的圆心P的坐标及半径r;
的伴圆的圆心P的坐标及半径r;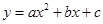 的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;
的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;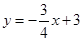 的所有伴圆的圆心P的坐标及半径.
的所有伴圆的圆心P的坐标及半径.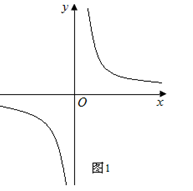
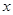 轴、
轴、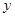 轴都相切的圆,则称⊙P是这个函数的伴圆.
轴都相切的圆,则称⊙P是这个函数的伴圆.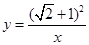 的伴圆的圆心P的坐标及半径r;
的伴圆的圆心P的坐标及半径r;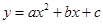 的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;
的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;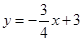 的所有伴圆的圆心P的坐标及半径.
的所有伴圆的圆心P的坐标及半径.