题目内容
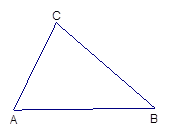
.如图,已知:在△ABC中,∠A=60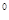 ,∠B=45
,∠B=45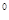 ,AB=8.求△ABC的面积(结果可保留根号)。
,AB=8.求△ABC的面积(结果可保留根号)。
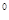 ,∠B=45
,∠B=45 ,AB=8.求△ABC的面积(结果可保留根号)。
,AB=8.求△ABC的面积(结果可保留根号)。
48-16

过C作CD⊥AB于D,利用直角三角形的性质求得CD的长.已知AB的长,根据三角形的面积公式即可求得其面积.
解答:解:过C作CD⊥AB于D,

在Rt△ADC中,∵∠CDA=90°,
∴ =cot∠DAC=cot60°=
=cot∠DAC=cot60°= ,
,
即AD=CD× .
.
在Rt△BDC中,∵∠B=45°,
∴∠BCD=45°,
∴CD=BD.
∵AB=DB+DA=CD+CD× =8,
=8,
∴CD=12-4 .
.
∴S△ABC= AB×CD=
AB×CD= ×8×(12-4
×8×(12-4 )=48-16
)=48-16 .
.
答:△ABC的面积为48-16 .
.
解答:解:过C作CD⊥AB于D,

在Rt△ADC中,∵∠CDA=90°,
∴
 =cot∠DAC=cot60°=
=cot∠DAC=cot60°= ,
,即AD=CD×
 .
.在Rt△BDC中,∵∠B=45°,
∴∠BCD=45°,
∴CD=BD.
∵AB=DB+DA=CD+CD×
 =8,
=8,∴CD=12-4
 .
.∴S△ABC=
 AB×CD=
AB×CD= ×8×(12-4
×8×(12-4 )=48-16
)=48-16 .
.答:△ABC的面积为48-16
 .
.
练习册系列答案
相关题目
 吗?
吗?
 与支架
与支架 所在直线相交于水箱横断面
所在直线相交于水箱横断面 的圆心
的圆心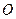 ,支架
,支架 垂直,
垂直, 厘米,
厘米, ,另一根辅助支架
,另一根辅助支架 厘米,
厘米, .
. 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据: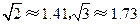 )
)



 ,则BC= 。
,则BC= 。
 °≈
°≈ ,
,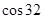 °≈
°≈ ,
, °≈
°≈ )
)


