题目内容
 如图梯形ABCD中,AD∥BC,∠ABC+∠C=90°,AB=6,CD=8,M,N,P分别为AD、BC、BD的中点,则MN的长为
如图梯形ABCD中,AD∥BC,∠ABC+∠C=90°,AB=6,CD=8,M,N,P分别为AD、BC、BD的中点,则MN的长为
- A.4
- B.5
- C.6
- D.7
B
分析:根据三角形的中位线定理,得MP∥AB,PN∥CD,MP= AB=3,PN=
AB=3,PN= CD=4;再根据平行线的性质,得∠MPD=∠ABD,∠PNB=∠C;根据三角形的外角的性质和已知∠ABC+∠C=90°,得∠MPN=90°,进而根据勾股定理求解.
CD=4;再根据平行线的性质,得∠MPD=∠ABD,∠PNB=∠C;根据三角形的外角的性质和已知∠ABC+∠C=90°,得∠MPN=90°,进而根据勾股定理求解.
解答:∵M,N,P分别为AD、BC、BD的中点,
∴MP∥AB,PN∥CD,MP= AB=3,PN=
AB=3,PN= CD=4.
CD=4.
∴∠MPD=∠ABD,∠PNB=∠C.
又∠ABC+∠C=90°,∠DPN=∠PBN+∠PNB,
∴∠MPN=90°.
∴MN= =5.
=5.
故选B.
点评:此题考查了三角形的中位线定理、三角形的外角的性质以及勾股定理.
分析:根据三角形的中位线定理,得MP∥AB,PN∥CD,MP=
 AB=3,PN=
AB=3,PN= CD=4;再根据平行线的性质,得∠MPD=∠ABD,∠PNB=∠C;根据三角形的外角的性质和已知∠ABC+∠C=90°,得∠MPN=90°,进而根据勾股定理求解.
CD=4;再根据平行线的性质,得∠MPD=∠ABD,∠PNB=∠C;根据三角形的外角的性质和已知∠ABC+∠C=90°,得∠MPN=90°,进而根据勾股定理求解.解答:∵M,N,P分别为AD、BC、BD的中点,
∴MP∥AB,PN∥CD,MP=
 AB=3,PN=
AB=3,PN= CD=4.
CD=4.∴∠MPD=∠ABD,∠PNB=∠C.
又∠ABC+∠C=90°,∠DPN=∠PBN+∠PNB,
∴∠MPN=90°.
∴MN=
 =5.
=5.故选B.
点评:此题考查了三角形的中位线定理、三角形的外角的性质以及勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图梯形ABCD中,AD∥BC,AB=DC=2,∠ABC=60°,且BD⊥AC,EF是梯形的中位线,求EF的长.
如图梯形ABCD中,AD∥BC,AB=DC=2,∠ABC=60°,且BD⊥AC,EF是梯形的中位线,求EF的长.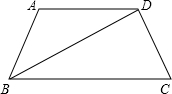 如图梯形ABCD中,AD∥BC,AB=AD=CD,BD⊥CD,求∠C的度数.
如图梯形ABCD中,AD∥BC,AB=AD=CD,BD⊥CD,求∠C的度数. 20、如图梯形ABCD中,∠B=60°,AB=5cm,将AB向右平移到点D,交BC于E,那么DE=
20、如图梯形ABCD中,∠B=60°,AB=5cm,将AB向右平移到点D,交BC于E,那么DE=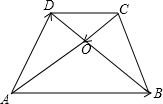
 15、如图梯形ABCD中,AD∥BC,AE∥DC,AD=5cm,梯形ABCD的周长为60cm,则△ABE的周长为( )
15、如图梯形ABCD中,AD∥BC,AE∥DC,AD=5cm,梯形ABCD的周长为60cm,则△ABE的周长为( )