题目内容
 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是
- A.10
- B.

- C.10或

- D.10或
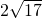
C
分析:先根据题意画出图形,再根据勾股定理求出斜边上的中线,最后即可求出斜边的长.
解答:①如图:

因为CD= =2
=2 ,
,
点D是斜边AB的中点,
所以AB=2CD=4 ,
,
②如图:

因为CE= =5,
=5,
点E是斜边AB的中点,
所以AB=2CE=10,
原直角三角形纸片的斜边长是10或 ,
,
故选C.
点评:此题考查了图形的剪拼,解题的关键是能够根据题意画出图形,在解题时要注意分两种情况画图,不要漏解.
分析:先根据题意画出图形,再根据勾股定理求出斜边上的中线,最后即可求出斜边的长.
解答:①如图:

因为CD=
 =2
=2 ,
,点D是斜边AB的中点,
所以AB=2CD=4
 ,
,②如图:

因为CE=
 =5,
=5,点E是斜边AB的中点,
所以AB=2CE=10,
原直角三角形纸片的斜边长是10或
 ,
,故选C.
点评:此题考查了图形的剪拼,解题的关键是能够根据题意画出图形,在解题时要注意分两种情况画图,不要漏解.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
 (2012•安徽)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( )
(2012•安徽)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( ) (2013•江宁区一模)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的面积是
(2013•江宁区一模)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的面积是
 如图,在一张直角三角形纸片,两直角边AC=6,BC=8,将△ABC折叠,使点B与点A重合,折痕为DE,则CD长为( )
如图,在一张直角三角形纸片,两直角边AC=6,BC=8,将△ABC折叠,使点B与点A重合,折痕为DE,则CD长为( ) 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为9、12、16,则原直角三角形纸片的斜边长是( )
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为9、12、16,则原直角三角形纸片的斜边长是( )