题目内容
四边形的四边依次是a、b、c、d,且满足(a-c)2+(b-d)2=0,此四边形是
- A.矩形
- B.菱形
- C.平行四边形
- D.等腰梯形
C
分析:由(a-c)2+(b-d)2=0可得a=c,b=d,四边形中两组对边相等,故可判定是平行四边形.
解答:∵(a-c)2+(b-d)2=0,
∴a=c,b=d
∵a,b,c,d分别为四边形ABCD的四边,
即两组对边分别相等,
∴四边形平行四边形.
故选C.
点评:此题主要考查平行四边形的判定问题,正确找出四边a、b、c、d的关系,熟练掌握平行四边形的判定定理是解题的关键.
分析:由(a-c)2+(b-d)2=0可得a=c,b=d,四边形中两组对边相等,故可判定是平行四边形.
解答:∵(a-c)2+(b-d)2=0,
∴a=c,b=d
∵a,b,c,d分别为四边形ABCD的四边,
即两组对边分别相等,
∴四边形平行四边形.
故选C.
点评:此题主要考查平行四边形的判定问题,正确找出四边a、b、c、d的关系,熟练掌握平行四边形的判定定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
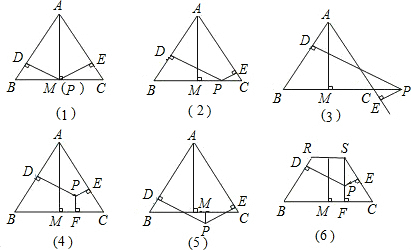
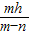 .图(4)与图(6)中的等式有何关系.
.图(4)与图(6)中的等式有何关系.