题目内容
若△ABC的边长为a、b、c，且满足a2+b2+c2=ab+bc+ca，则△ABC的形状是
- A.等腰三角形
- B.等边三角形
- C.任意三角形
- D.不能确定
B
分析：利用完全平方公式进行局部因式分解，再根据非负数的性质进行分析．
解答：∵a2+b2+c2=ab+bc+ca，
∴2a2+2b2+2c2-2ab-2bc-2ca=0，
（a-b）2+（a-c）2+（b-c）2=0，
∴a=b=c，
∴三角形是等边三角形．
故选B．
点评：此题考查了完全平方公式的运用和非负数的性质，即几个非负数的和为0，则这几个非负数同时为0．
分析：利用完全平方公式进行局部因式分解，再根据非负数的性质进行分析．
解答：∵a2+b2+c2=ab+bc+ca，
∴2a2+2b2+2c2-2ab-2bc-2ca=0，
（a-b）2+（a-c）2+（b-c）2=0，
∴a=b=c，
∴三角形是等边三角形．
故选B．
点评：此题考查了完全平方公式的运用和非负数的性质，即几个非负数的和为0，则这几个非负数同时为0．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
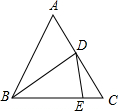如图，△ABC为等边三角形，D，E分别是边AC，BC上的点（不与顶点重合），∠BDE=60°，若△ABC的边长为6，设DC=x，BE=y，则y与x之间的函数关系式是（ ）
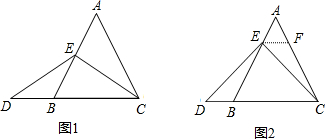
如图，△ABC是等边三角形，D为AB边上的一个动点，DE∥BC，延长BC到F，使CF=AD，连接DF交AC于P．