题目内容
（2013•内江）如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为3米，台阶AC的坡度为1：| 3 |
| 3 |
分析：过点A作AF⊥DE于F，可得四边形ABEF为矩形，设DE=x，在Rt△DCE和Rt△ABC中分别表示出CE，BC的长度，求出DF的长度，然后在Rt△ADF中表示出AF的长度，根据AF=BE，代入解方程求出x的值即可．
解答：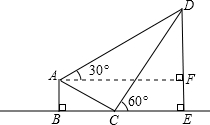
解：如图，过点A作AF⊥DE于F，
则四边形ABEF为矩形，
∴AF=BE，EF=AB=3，
设DE=x，
在Rt△CDE中，CE=
=
x，
在Rt△ABC中，
∵
=
，AB=3，
∴BC=3
，
在Rt△AFD中，DF=DE-EF=x-3，
∴AF=
=
（x-3），
∵AF=BE=BC+CE，
∴
（x-3）=3
+
x，
解得x=9．
答：树高为9米．
解：如图，过点A作AF⊥DE于F，则四边形ABEF为矩形，
∴AF=BE，EF=AB=3，
设DE=x，
在Rt△CDE中，CE=
| DE |
| tan60° |
| ||
| 3 |
在Rt△ABC中，
∵
| AB |
| BC |
| 1 | ||
|
∴BC=3
| 3 |
在Rt△AFD中，DF=DE-EF=x-3，
∴AF=
| x-3 |
| tan30° |
| 3 |
∵AF=BE=BC+CE，
∴
| 3 |
| 3 |
| ||
| 3 |
解得x=9．
答：树高为9米．
点评：本题考查了解直角三角形的应用，解题的关键是正确的构造直角三角形并选择正确的边角关系解直角三角形，难度一般．
练习册系列答案
相关题目
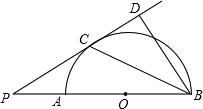（2013•内江）如图，AB是半圆O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC．
（2013•内江）如图，反比例函数
（2013•内江）如图，正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置，若正六边形的边长为2cm，则正六边形的中心O运动的路程为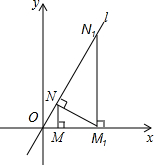
（2013•内江）如图，已知直线l：y=