题目内容
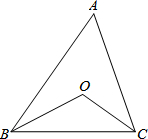 如图,在△ABC中,∠ABC,∠ACB的角平分线相交于O点.
如图,在△ABC中,∠ABC,∠ACB的角平分线相交于O点.(1)如果∠A=80°,那么∠BOC的度数为
(2)如果∠A=α,那么∠BOC的度数为
考点:三角形内角和定理
专题:
分析:(1)根据三角形的内角和定理求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形的内角和定理列式计算即可得解;
(2)根据(1)的思路把∠A的度数化为α计算即可得解.
(2)根据(1)的思路把∠A的度数化为α计算即可得解.
解答:解:(1)∵∠A=80°,
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵∠ABC,∠ACB的角平分线相交于点O,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×100°=50°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°;
(2)∵∠A=α,
∴∠ABC+∠ACB=180°-∠A=180°-α,
∵∠ABC,∠ACB的角平分线相交于点O,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
(180°-α)=90°-
α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-
α)=90°+
α.
故答案为:130°,90°+
α.
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵∠ABC,∠ACB的角平分线相交于点O,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°;
(2)∵∠A=α,
∴∠ABC+∠ACB=180°-∠A=180°-α,
∵∠ABC,∠ACB的角平分线相交于点O,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:130°,90°+
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
相关题目
△ABC的顶点A的坐标为(-2,4),先将△ABC沿x轴对折,再向左平移两个单位,此时A点的坐标为( )
| A、(2,-4) |
| B、(0,-4) |
| C、(-4,-4) |
| D、(0,4) |
若抛物线y=ax2-2x+3的顶点坐标为(2,-3),则该抛物线有( )
| A、最大值-3 | B、最小值-3 |
| C、最大值2 | D、最小值2 |
下列图形中既是中心对称图形又是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
点(-4,-2)关于y轴对称的点的坐标是( )
| A、(4,2) |
| B、(-4,2) |
| C、(-4,-2) |
| D、(4,-2) |
抛物线y=ax2+bx和直线y=ax+b在同一坐标系的图象可能是( )
A、 |
B、 |
C、 |
D、 |
下列各式从左到右的变形中,是因式分解的是( )
A、m2-2m-3=m(m-2-
| ||
| B、a2+2a+2=(a+1)2+1 | ||
| C、x2-1=(x+1)(x-1) | ||
| D、x2-y2=(x+y)(x-y)=x2-y2 |
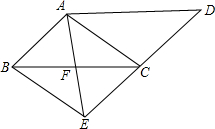 如图,将平行四边形ABCD的边延长线到点E,使CE=DC,连接AE,交BC于点F.
如图,将平行四边形ABCD的边延长线到点E,使CE=DC,连接AE,交BC于点F.