题目内容
如图1,△ABC中,AB=AC,BD⊥AC于D.
(1)若∠A=40゜,则∠DBC=
α
α;
(2)如图2,猜想:∠DBC与∠BAC之间的数量关系,并予以证明.

(1)若∠A=40゜,则∠DBC=
20゜
20゜
;若∠A=50゜,则∠DBC=25゜
25゜
;若∠A=α,则∠DBC=| 1 |
| 2 |
| 1 |
| 2 |
(2)如图2,猜想:∠DBC与∠BAC之间的数量关系,并予以证明.

分析:(1)由AB=AC,BD⊥AC,可求得∠ABC与∠ABD的度数,继而求得∠DBC的度数;
(2)首先设∠C=β,由等腰三角形的性质,可求得∠BAC与∠DBC的值,继而求得:∠DBC与∠BAC之间的数量关系.
(2)首先设∠C=β,由等腰三角形的性质,可求得∠BAC与∠DBC的值,继而求得:∠DBC与∠BAC之间的数量关系.
解答:解:(1)∵AB=AC,∠A=α,
∴∠ABC=∠C=
=
=90°-
α,
∵BD⊥AC,
∴∠ABD=90°-α,
∴∠DBC=∠ABC-∠ABD=
α;
当∠A=40゜时,∠DBC=20°;
当∠A=50°时,∠DBC=25°;
故答案为:20°,25°,
α;
(2)∠DBC=
∠BAC.
设∠C=β,
∵AB=AC,
∴∠ABC=∠C=β,
∴∠BAC=180°-2β,∠BAD=∠ABC+∠C=2β,
∵BD⊥AC,
∴∠ABD=90°-2β,
∴∠DBC=90゜-β,
∴∠DBC=
∠BAC.
∴∠ABC=∠C=
| 180°-∠A |
| 2 |
| 180°-α |
| 2 |
| 1 |
| 2 |
∵BD⊥AC,
∴∠ABD=90°-α,
∴∠DBC=∠ABC-∠ABD=
| 1 |
| 2 |
当∠A=40゜时,∠DBC=20°;
当∠A=50°时,∠DBC=25°;
故答案为:20°,25°,
| 1 |
| 2 |
(2)∠DBC=
| 1 |
| 2 |
设∠C=β,
∵AB=AC,
∴∠ABC=∠C=β,
∴∠BAC=180°-2β,∠BAD=∠ABC+∠C=2β,
∵BD⊥AC,
∴∠ABD=90°-2β,
∴∠DBC=90゜-β,
∴∠DBC=
| 1 |
| 2 |
点评:此题考查了等腰三角形的性质、三角形外角的性质以及三角形内角和定理.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
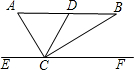 如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )
如图,Rt△ABC中,DC是斜边AB上的中线,EF过点C且平行于AB.若∠BCF=35°,则∠ACD的度数是( )| A、35° | B、45° | C、55° | D、65° |
 17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有:
17、如图,在△ABC中,AB=AC,AD是△ABC的平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B、C两点距离相等;④图中共有3对全等三角形,正确的有: 8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )
8、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是( )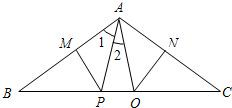 如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数.
如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数. 19、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.
19、如图,在△ABC中,∠C=90°,DE⊥AB于E,DF⊥BC于F.求证:△DEH∽△BCA.