题目内容
4．
如图，Rt△ABC中，∠B=90°，∠A=30°，AB=5，D是AC的中点，P是AB上一动点，则CP+PD的最小值为5．
分析 作C关于AB的对称点C'，连接C′D，易求∠ACC'=60°，则AC=AC'，且△ACC'为等边三角形，CP+PD=DP+PC'为C'与直线AC之间的连接线段，其最小值为C'到AC的距离=AB=5，所以最小值为5．
解答 解：作C关于AB的对称点C'，连接C′D，
∵∠B=90°，∠A=30°，
∴∠ACB=60°，
∵AC=AC'，
∴△ACC'为等边三角形，
∴CP+PD=DP+PC'为C'与直线AC之间的连接线段，
∴最小值为C'到AC的距离=AB=5，
故答案为：5．
点评 本题考查的是最短线路问题及等边三角形的性质，熟知两点之间线段最短的知识是解答此题的关键．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
下列图形由5个大小一样正方体组成，画出该立体图形的三视图．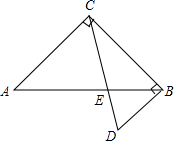
如图，将两块直角三角形的一条直角边重合叠放，已知AC=BC=$\sqrt{3}$+1，∠D=60°，则两条斜边的交点E到直角边BC的距离是1．
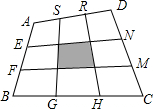如图，已知四边形ABCD中E，F，G，H，N、N，R、S分别是四边形三等分点，求证：S阴影=$\frac{1}{9}$S四边形ABCD．
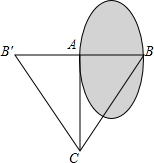如图，测量水池的宽AB，可过点A作直线AC⊥AB，再由点C观测，在BA延长线上找一点B′，使∠ACB′=∠ACB，这时只要量出AB′的长，就知道AB的长，这个测量用到三角形全等判定方法是ASA．
如图，某拦河坝横截面原设计方案为梯形ABCD，其中AD∥BC，∠ABC=72°，为了提高拦河坝的安全性，现将坝顶宽度水平缩短10m，坝底宽度水平增加4m，使∠EFC=45°，请你计算这个拦河大坝的高度．（参考数据：sin72°≈$\frac{12}{13}$，cos72°≈$\frac{5}{13}$，tan72°$≈\frac{12}{5}$）
13．某区从参加地理学业水平考试的8000名学生中，随机抽取了部分学生的成绩作为样本，为了节省时间，先将样本分成甲、乙两组，分别进行分析，得到下表；随后汇总整个样本数据，得到部分结果，绘制成如下统计图．
（注：A：优秀（≥90分）、B：良好（≥70分且＜90分）、C：及格（≥60分且＜70分）、D：不及格（＜60分））
表一
请根据图和表所示信息回答下列问题：
（1）样本中，学生地理学成绩平均分为B分，中位数在B内（填等第），众数是
B（填等第）．A占的百分比是30%，C占的百分比是15%．
（2）补全条形统计图．
（3）成绩不低于60的为合格，估计这8000名学生的合格人数．
（注：A：优秀（≥90分）、B：良好（≥70分且＜90分）、C：及格（≥60分且＜70分）、D：不及格（＜60分））
表一
| 甲组 | 乙组 | |
| 人数（人） | 120 | 80 |
| 平均分（分） | 88 | 83 |
（1）样本中，学生地理学成绩平均分为B分，中位数在B内（填等第），众数是
B（填等第）．A占的百分比是30%，C占的百分比是15%．
（2）补全条形统计图．
（3）成绩不低于60的为合格，估计这8000名学生的合格人数．
如图是某几何体的三视图，根据图中数据，求得该几何体的体积为70π．（结果保留π）