Question

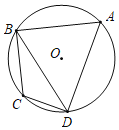
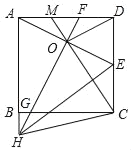
【题目】如图，正方形中，为的中点，的垂直平分线分别交，及的延长线于点，，，连接，，，连接并延长交于点，则下列结论中：①；②；③；④；⑤ ；⑥；⑦．正确的结论的个数为（ ）

A.3B.4C.5D.6

Answer 1

【答案】B

【解析】

①作辅助线，构建三角形全等，证明△ADE≌△GKF，则FG=AE，可得FG=2AO；

②设正方形ABCD的边长为2x，则AD=AB=2x，DE=EC=x，证明△ADE∽△HOA，得，于是可求BH及HE的值，可作出判断；

③分别表示出OD、OC，根据勾股定理逆定理可以判断；

④证明∠HEA=∠AED=∠ODE，OE≠DE，则∠DOE≠∠HEA，OD与HE不平行；
⑤由②可得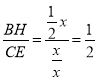，根据AR∥CD，得，则；

⑥证明△HAE∽△ODE，可得，等量代换可得OE2=AHDE；

⑦分别计算HC、OG、BH的长，可得结论．

解：①如图，过G作GK⊥AD于K，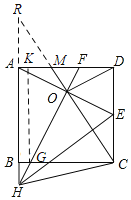

∴∠GKF=90°，
∵四边形ABCD是正方形，
∴∠ADE=90°，AD=AB=GK，
∴∠ADE=∠GKF，
∵AE⊥FH，
∴∠AOF=∠OAF+∠AFO=90°，
∵∠OAF+∠AED=90°，
∴∠AFO=∠AED，
∴△ADE≌△GKF，
∴FG=AE，
∵FH是AE的中垂线，
∴AE=2AO，
∴FG=2AO，
故①正确；

②设正方形ABCD的边长为2x，则AD=AB=2x，DE=EC=x，

，

易得△ADE∽△HOA，

，

，

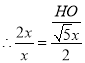Rt△AHO中，由勾股定理得：AH= ，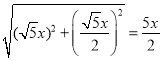

∴BH=AH-AB= ，

∵HE=AH= ，

∴HE=5BH；
故②正确；

③，，

∴，

∴OC与OD不垂直，

故③错误；
④∵FH是AE的中垂线，
∴AH=EH，
∴∠HAE=∠HEA，
∵AB∥CD，
∴∠HAE=∠AED，
Rt△ADE中，∵O是AE的中点，
∴OD=AE=OE，
∴∠ODE=∠AED，
∴∠HEA=∠AED=∠ODE，
当∠DOE=∠HEA时，OD∥HE，
但AE＞AD，即AE＞CD，
∴OE＞DE，即∠DOE≠∠HEA，
∴OD与HE不平行，
故④不正确；
⑤由②知BH=，

，

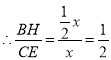延长CM、BA交于R，

∵RA∥CE，
∴∠ARO=∠ECO，
∵AO=EO，∠ROA=∠COE，
∴△ARO≌△ECO，
∴AR=CE，
∵AR∥CD，

，

故⑤正确；
⑥由①知：∠HAE=∠AEH=∠OED=∠ODE，
∴△HAE∽△ODE，

∵AE=2OE，OD=OE，
∴OE2OE=AHDE，
∴2OE2=AHDE，
故⑥正确；
⑦由②知：HC= ，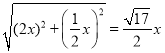

∵AE=2AO=OH= ，

tan∠EAD= ，

，

，

∵FG=AE ，

，

∴OG+BH= ，

∴OG+BH≠HC，
故⑦不正确；
综上所述，本题正确的有；①②⑤⑥，共4个，
故选：B．