题目内容
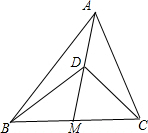在△ABC中，D是中线AM上一点，若∠DCB＞∠DBC，求证：∠ACB＞∠ABC（如图）．
证明：∵在△BCD中，∠DCB＞∠DBC，
∴BD＞CD．
∴∠DMB＞∠DMC．
∵∠AMB＞∠AMC，
∴AB＞AC，
∴∠ACB＞∠ABC．
分析：在证明角的不等式时，常常把角的不等式转换成边的不等式，根据大角对大边可得到BD＞CD，在△DMB与△DMC中，DM为公共边，BM=MC，BD＞CD，从而可推出∠DMB＞∠DMC，同理可证得AB＞AC，从而不难证得结论．
点评：此题主要考查三角形三边关系的理解及运用能力，注意在证明角的不等式时，常常把角的不等式转换成边的不等式．
∴BD＞CD．
∴∠DMB＞∠DMC．
∵∠AMB＞∠AMC，
∴AB＞AC，
∴∠ACB＞∠ABC．
分析：在证明角的不等式时，常常把角的不等式转换成边的不等式，根据大角对大边可得到BD＞CD，在△DMB与△DMC中，DM为公共边，BM=MC，BD＞CD，从而可推出∠DMB＞∠DMC，同理可证得AB＞AC，从而不难证得结论．
点评：此题主要考查三角形三边关系的理解及运用能力，注意在证明角的不等式时，常常把角的不等式转换成边的不等式．
练习册系列答案
相关题目
在△ABC中，AD是BC上的高，且AD=
BC，E，F分别是AB，AC的中点，以EF为直径的圆与BC的位置关系是（ ）
| 1 |
| 2 |
| A、相离 | B、相切 |
| C、相交 | D、相切或相交 |
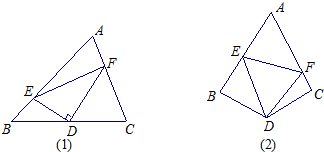
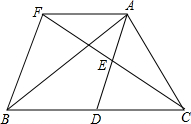如图，在△ABC中，AD是中线，点E是AD的中点，过A点作BC的平行线交CE的延长线于点F，连接BF．