题目内容
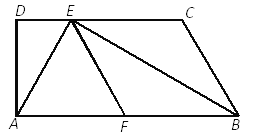
【题目】如图,以矩形![]() 的顶点
的顶点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.已知,
轴,建立平面直角坐标系.已知,![]() ,
,![]() ,点
,点![]() 为
为![]() 轴上一动点,以
轴上一动点,以![]() 为一边在
为一边在![]() 右侧作正方形
右侧作正方形![]() .
.
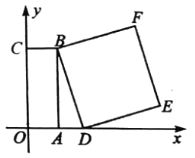
(1)若点![]() 与点
与点![]() 重合,请直接写出点
重合,请直接写出点![]() 的坐标.
的坐标.
(2)若点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
(1)![]() 与点
与点![]() 重合则点E为(6,3)
重合则点E为(6,3)
(2)![]() 作
作![]() 轴,证明:
轴,证明:![]() 即
即![]() 则点E为(8,3)
则点E为(8,3)
(3)分情况解答,![]() 在点
在点![]() 右侧,过点
右侧,过点![]() 作
作![]() 轴,证明:
轴,证明:![]() ;
;![]() 在点
在点![]() 左侧,点
左侧,点![]() 作
作![]() 轴,证明:
轴,证明:![]()
解:(1)![]()
![]() 与点
与点![]() 重合则点E再x轴的位置为2+4=6
重合则点E再x轴的位置为2+4=6
![]()
![]() .
.
(2)过点![]() 作
作![]() 轴,
轴,
∵∠BAD=∠EMD=∠BDE=90°,
∴∠BDA+∠ABD=∠BDA+∠MDE,
∴∠ABD=∠MDE,
∵BD=DE,
![]()

![]() ,
,![]() 点
点![]() 在线段
在线段![]() 的中垂线上,
的中垂线上,![]() .
.
![]() ,
,![]() .
.
![]() .
.
![]()
(3)①点![]() 在点
在点![]() 右侧,如图,
右侧,如图,

过点![]() 作
作![]() 轴,同(2)
轴,同(2)![]()
设![]() ,可得:
,可得:![]() ,
,![]()
![]()
求得:![]() ,
,![]() (舍去)
(舍去)
![]()
②点![]() 在点
在点![]() 左侧,如图,
左侧,如图,
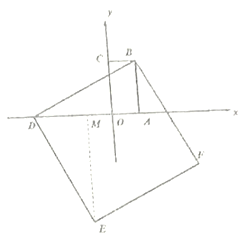
过点![]() 作
作![]() 轴,同上得
轴,同上得![]()
设![]() ,可得:
,可得:![]() ,
,![]()
![]() ,
,
求得:![]() ,
,![]() (舍去)
(舍去)
![]()
综上所述:![]() ,
,![]()

练习册系列答案
相关题目