题目内容
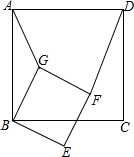如图，四边形ABCD和BEFG均为正方形，则| AG |
| DF |
考点：相似三角形的判定与性质,正方形的性质
专题：
分析：连接BD、BF，结合正方形的性质可证明△ABG∽△DBF，进一步可求得
．
| AG |
| DF |
解答：
解：如图，连接BF，BD，
∵四边形ABCD和BEFG均为正方形，
∴BD=
AB，BF=
BG，∠ABD=∠CBF=45°，
∴
=
，且∠ABG+∠GBD=∠DBF+∠GBD，即∠ABG=∠DBF，
∴△ABG∽△DBF，
∴
=
=
，
故答案为：
．
解：如图，连接BF，BD，∵四边形ABCD和BEFG均为正方形，
∴BD=
| 2 |
| 2 |
∴
| AB |
| BG |
| BD |
| BF |
∴△ABG∽△DBF，
∴
| AG |
| DF |
| BG |
| BF |
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题主要考查了相似三角形的判定和性质，解答本题要充分利用正方形的特殊性质．
练习册系列答案
相关题目
如图所示，用5个小正方体搭成的立体图形，请你从正面、左面、上面观察这个几何体，分别画出你所看到的几何体的形状图．
在平面直角坐标系中，抛物线y=x2+bx+c与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点B的坐标为（3，0），将直线y=kx沿y轴向上平移3个单位长度后恰好经过B、C两点．
如图，在四边形ABCD中，AB∥DC，AH⊥DC于H，CP⊥BD于P，CP延长线分别交AH、AD于E、F，DB平分∠ABC，HE=BP．
如图，从等腰△ABC内一点P，向两腰AB、AC作垂线，垂足分别为D、E，向底边BC作垂线，垂足为F，若PD+PE=PF．求适合条件的点P的轨迹．
（1）在数轴上表示下列各数