题目内容
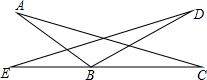如图，△ABC绕点B逆时针方向旋转到△EBD的位置，若∠A=15°，∠C=10°，E、B、C在同一直线上，则旋转角是（ ）| A、10° | B、15° |
| C、20° | D、25° |
考点：旋转的性质
专题：
分析：在△ABC中，已知∠A=15°、∠C=10°，根据内角和定理可求∠ABC；点B为旋转中心，E的对应点为A，故旋转角为∠ABE，由互补关系可求∠ABE．
解答：解：在△ABC中，已知∠A=15°，∠C=10°，
∴∠ABC=180°-∠A-∠C=155°；
又∵点B为旋转中心，E的对应点为A，
∴旋转角为∠ABE=180°-∠ABC=25°．
故选D．
∴∠ABC=180°-∠A-∠C=155°；
又∵点B为旋转中心，E的对应点为A，
∴旋转角为∠ABE=180°-∠ABC=25°．
故选D．
点评：本题考查了三角形内角和定理的运用，旋转的基本概念和性质，需要熟练掌握．
练习册系列答案
相关题目
如图，货轮与灯塔相距30海里，如何用方向和距离描述货轮相对于灯塔的位置下列各数中：
，0，-
，
，0.3，0.3030030003…，
，无理数有（ ）
| 3 | -1 |
| 0.4 |
| 9 |
| 1 |
| π |
| A、0个 | B、1个 | C、2个 | D、3个 |
若2是关于方程x2-5x+c=0的一个根，则这个方程的另一个根是（ ）
| A、-3 | B、3 | C、-6 | D、6 |
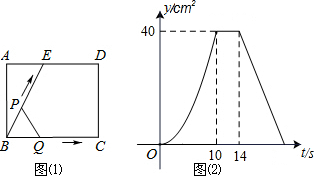如图（1），E为矩形ABCD边AD上一点，点P从点B沿折线BE-ED-DC运动到点C时停止，点Q从点B沿BC运动到点C时停止，它们运动的速度都是1cm/s．如果点P、Q同时开始运动，设运动时间为t（s），△BPQ的面积为y（cm2），已知y与t的函数关系的图象如图（2）所示，那么下列结论正确的是（ ）| A、AE=8 | ||
B、当0≤t≤10时，y=
| ||
C、sin∠EBD=
| ||
| D、当t=12s时，△BPQ是等腰三角形 |
把分式
中的x和y都扩大为原来的3倍，那么分式的值（ ）
| x2 |
| 2x+y |
| A、不变 |
| B、扩大为原来的3倍 |
| C、扩大为原来的6倍 |
| D、扩大为原来的9倍 |
⊙O1的半径为4，⊙O2的半径为3，两圆的圆心距O1O2=1，则两圆的位置关系是（ ）
| A、内含 | B、内切 | C、相交 | D、外切 |
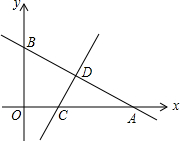如图，一次函数y=kx+n的图象与x轴和y轴分别交于点A（6，0）和B（0，2