Question

【题目】一租赁公司拥有某种型号的汽车10辆，公司在经营中发现每辆汽车每天的租赁价为120元时可全部出租，租赁价每涨3元就少出租1辆，公司决定采取涨价措施．

填空：每天租出的汽车数辆与每辆汽车的租赁价元之间的关系式为______．

已知租出的汽车每辆每天需要维护费30元，求租出汽车每天的实际收入元与每辆汽车的租赁价元之间的关系式；租出汽车每天的实际收入租出收入租出汽车维护费

若未租出的汽车每辆每天需要维护费12元，则每辆汽车每天的租赁价元定为多少元时，才能使公司获得日收益元最大？并求出公司的最大日收益．

Answer 1

【答案】（1）（2）；（3）将每辆汽车的日租金定为120元，才能使公司获得最大日收益，公司的最大日收益是900元．

【解析】

（1）判断出y与x的函数关系为一次函数关系，再根据待定系数法求出函数解析式；

（2）根据租出汽车每天的实际收入＝租出收入﹣租出汽车维护费即可得到结论；

（3）租出的车的利润减去未租出车的维护费，即为公司月收益，再利用二次函数的性质求解可得．

解：根据题意得，y与x满足一次函数关系，设，

则，

解得：，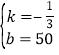

即每天租出的汽车数辆与每辆汽车的租赁价元之间的关系式为：；

故答案为：；

设公司获得的日收益为w，

则

；

，

当时，z随x的增大而减小，

当时，z取得最大值，最大值，

答：将每辆汽车的日租金定为120元，才能使公司获得最大日收益，公司的最大日收益是900元．