Question

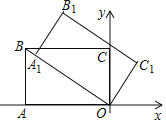
【题目】如图，在平面直角坐标系中，矩形OABC的顶点A（﹣3，0），C（0，）．将矩形OABC绕点O顺时针方向旋转，使点A恰好落在OB上的点A1处，则点B的对应点B1的坐标为_____．

Answer 1

【答案】（﹣，3）

【解析】

连接OB1，作B1H⊥OA于H，证明△AOB≌△HB1O，得到B1H＝OA＝3，OH＝AB＝，得到答案．

解：连接OB1，作B1H⊥OA于H，如图所示：

由题意得，OA＝3，AB＝OC＝，

则tan∠BOA＝＝，

∴∠BOA＝30°，

∴∠OBA＝60°，

由旋转的性质可知，∠B1OB＝∠BOA＝30°，

∴∠B1OH＝60°，

在△AOB和△HB1O中，

，

∴△AOB≌△HB1O（AAS），

∴B1H＝OA＝3，OH＝AB＝，

∴点B1的坐标为（﹣，3），

故答案为：（﹣，3）．