题目内容
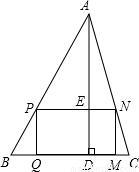
如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积.
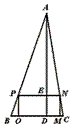
解:∵ 矩形PQMN,
∴ PN∥QM,PN=QM.∵ AD⊥BC,
∴ AE⊥PN.∵ △APN∽△ABC,
∴ =
= .
.
设ED=x,又 矩形周长为24,则 PN=12-x,AD=16+x.
∴ .即 x2+4x-32=0.
.即 x2+4x-32=0.
解得 x=4.
∴ AD=AE+ED=20.
∴ S△ABC= BC·AD=100.
BC·AD=100.
∴ PN∥QM,PN=QM.∵ AD⊥BC,
∴ AE⊥PN.∵ △APN∽△ABC,
∴
 =
= .
. 设ED=x,又 矩形周长为24,则 PN=12-x,AD=16+x.
∴
 .即 x2+4x-32=0.
.即 x2+4x-32=0.解得 x=4.
∴ AD=AE+ED=20.
∴ S△ABC=
 BC·AD=100.
BC·AD=100. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
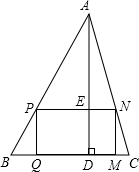 如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积.
如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积. 如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积.
如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积.