题目内容
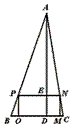
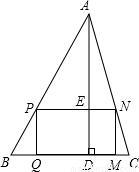
 如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积.
如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积.
解:∵矩形PQMN,
∴PN∥QM,PN=QM
∵AD⊥BC,
∴AE⊥PN
∵△APN∽△ABC,
∴
设ED=x,又矩形周长为24,则
PN=12-x,AD=16+x
∴ =
= 即x2+4x-32=0,
即x2+4x-32=0,
解得x=4
∴AD=AE+ED=20,
∴S△ABC= BC•AD=100.
BC•AD=100.
分析:求△ABC的面积,即求出底边BC与高AD即可,因为△APN∽△ABC,所以可得对应边成比例,可设DE=x,用未知数代入求解即可.
点评:能够熟练运用相似三角形的性质,会运用对应边成比例求解一些简单的计算问题.
∴PN∥QM,PN=QM
∵AD⊥BC,
∴AE⊥PN
∵△APN∽△ABC,
∴

设ED=x,又矩形周长为24,则
PN=12-x,AD=16+x
∴
 =
= 即x2+4x-32=0,
即x2+4x-32=0,解得x=4
∴AD=AE+ED=20,
∴S△ABC=
 BC•AD=100.
BC•AD=100.分析:求△ABC的面积,即求出底边BC与高AD即可,因为△APN∽△ABC,所以可得对应边成比例,可设DE=x,用未知数代入求解即可.
点评:能够熟练运用相似三角形的性质,会运用对应边成比例求解一些简单的计算问题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
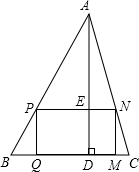 如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积.
如图,矩形PQMN内接于△ABC,矩形周长为24,AD⊥BC交PN于E,且BC=10,AE=16,求△ABC的面积.