题目内容
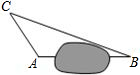 在一次课外实践活动中,同学们要知道校园内A,B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,现测得AC=6m,BC=14m,∠CAB=120°,请计算A,B两处之间的距离.
在一次课外实践活动中,同学们要知道校园内A,B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,现测得AC=6m,BC=14m,∠CAB=120°,请计算A,B两处之间的距离.
分析:过C作CH⊥AB于H构造直角三角形,在两个直角三角形中分别求得BH、AH,相减即可求得AB的长.
解答: 解:过C作CH⊥AB于H,
解:过C作CH⊥AB于H,
∵∠CAB=120°,
∴∠CAH=60°,
∵AC=6,
∴AH=3,HC=3
,
在Rt△BCH中,∵BC=14,HC=3
,
∴BH=
=
=
=13
∴AB=BH-AH=13-3=10
即A,B两处之间的距离为10米.
 解:过C作CH⊥AB于H,
解:过C作CH⊥AB于H,∵∠CAB=120°,
∴∠CAH=60°,
∵AC=6,
∴AH=3,HC=3
| 3 |
在Rt△BCH中,∵BC=14,HC=3
| 3 |
∴BH=
| BC2-HC2 |
142-(3
|
| 169 |
∴AB=BH-AH=13-3=10
即A,B两处之间的距离为10米.
点评:本题考查了勾股定理的应用,解决本题的关键是作出钝角三角形的高,从而构造两个直角三角形,利用勾股定理解之.

练习册系列答案
相关题目
在一次课外实践活动中,有两个课题学习小组分别用测倾器、皮尺测量旗杆和小山的高度,他们分别设计了如下方案:
第一组,测量旗杆(图-):①在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=α;②量出测点A到旗杆底部N的水平距离AN=m;量出测倾器的高度AC=h.
第二组,测量某小山的高度(图二),他们测量时所填写的表格如下:
(1)请你求出旗杆的高度(用已知的字母表示);
(2)第二小组记录的同学不小心将AB的距离弄模糊了,请你填上一个较合理的数据,并由此求出小山PH的高度(结果精确到个位).
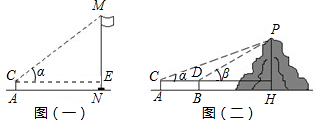
第一组,测量旗杆(图-):①在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=α;②量出测点A到旗杆底部N的水平距离AN=m;量出测倾器的高度AC=h.
第二组,测量某小山的高度(图二),他们测量时所填写的表格如下:
| 题目 | 测量小山的高度 | ||
| 测量数据 |
测量项目 | 测倾器高度 | |
| 仰角α | 20°30′ | 1.2米 | |
| 仰角β | 30° | 小山高度 | |
| AB的距离 | |||
(2)第二小组记录的同学不小心将AB的距离弄模糊了,请你填上一个较合理的数据,并由此求出小山PH的高度(结果精确到个位).

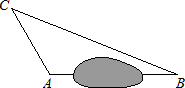 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=30m,BC=70m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=30m,BC=70m,∠CAB=120°,请计算A,B两个凉亭之间的距离.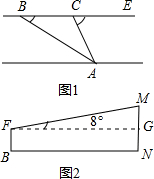 米到C处,再观察A,此时视线CA与河岸所成的夹角∠ACE=64°.
米到C处,再观察A,此时视线CA与河岸所成的夹角∠ACE=64°. 在一次课外实践活动中,同学们要知道校园内A、B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,现测得AC=6m,BC=14m,∠CAB=60°,请计算A、B两处之间的距离.
在一次课外实践活动中,同学们要知道校园内A、B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,现测得AC=6m,BC=14m,∠CAB=60°,请计算A、B两处之间的距离.