题目内容
6.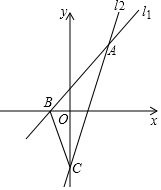 如图,直线l1、l2相交于点A(2,3),直线l1与x轴交点B的坐标为(-1,0),直线l2与y轴交于点C,已知直线l2的解析式为y=2.5x-2,结合图象解答下列问题:
如图,直线l1、l2相交于点A(2,3),直线l1与x轴交点B的坐标为(-1,0),直线l2与y轴交于点C,已知直线l2的解析式为y=2.5x-2,结合图象解答下列问题:(1)求直线l1的解析式;
(2)求△ABC的面积.
分析 (1)因为直线l1过点A(2,3),B(-1,0),所以可用待定系数法求得函数的表达式;
(2)先求得C点的坐标,然后根据S△ABC=S△ABD+S△BDC即可求得.
解答 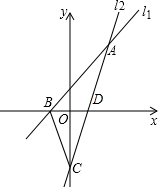 解:(1)设直线l1表示的一次函数表达式为y=kx+b,
解:(1)设直线l1表示的一次函数表达式为y=kx+b,
∵直线l1过点A(2,3),B(-1,0),
∴$\left\{\begin{array}{l}{2k+b=3}\\{-k+b=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线l2表示的一次函数表达式是y=x+1;
(2)设直线l2与x轴交于点D,由y=0,得2.5x-2=0,解得:x=$\frac{4}{5}$,
∴S△ABC=S△ABD+S△BDC=$\frac{1}{2}$×($\frac{4}{5}$+1)×3+$\frac{1}{2}$×($\frac{4}{5}$+1)×2=4.5.
点评 本题主要考查待定系数法求函数解析式,三角形面积的求法,掌握待定系数应用的关键是求得函数图象上的点的坐标.

练习册系列答案
相关题目
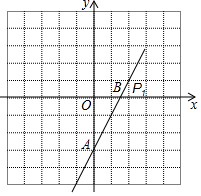 如图,直线l:y=mx-3与x轴、y轴分别交于点A、B,点P1(2,1)在直线l上,将点P1先向右平移1个单位,再向上平移2个单位得到像点P2.
如图,直线l:y=mx-3与x轴、y轴分别交于点A、B,点P1(2,1)在直线l上,将点P1先向右平移1个单位,再向上平移2个单位得到像点P2. 如图,数轴上A、B两点表示的数分别为$\sqrt{2}$和6.3,则A、B两点之间表示整数的点共有5个.
如图,数轴上A、B两点表示的数分别为$\sqrt{2}$和6.3,则A、B两点之间表示整数的点共有5个.