题目内容
4.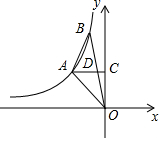 如图,A、B是反比例函数y=$\frac{k}{x}$图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为-$\frac{16}{3}$.
如图,A、B是反比例函数y=$\frac{k}{x}$图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为-$\frac{16}{3}$.
分析 过B作BE⊥y轴于E,得到CD∥BE,根据三角形中位线的性质得到CD=$\frac{1}{2}$BE,于是得到S△OBE=4S△OCD=-$\frac{1}{2}$k,求得S△OAD=2,根据反比例函数的系数k的几何意义得到S△OCD=-$\frac{1}{2}$k-2,于是得到结论.
解答  解:过B作BE⊥y轴于E,
解:过B作BE⊥y轴于E,
∵BE⊥y轴,AC⊥y轴,
∴CD∥BE,
∵D为OB的中点,
∴OD=BD,
∴OC=CE,
∴CD=$\frac{1}{2}$BE,
∴S△OBE=4S△OCD=-$\frac{1}{2}$k,
∵△ABO的面积为4,
∴S△OAD=2,
∵S△AOC=-$\frac{1}{2}$k,
∴S△OCD=-$\frac{1}{2}$k-2,
∴-$\frac{1}{8}$k=-$\frac{1}{2}$k-2,
∴k=-$\frac{16}{3}$,
故答案为:-$\frac{16}{3}$.
点评 本题考查了反比例函数的系数k的几何意义,三角形的中位线的性质,三角形面积的计算,正确的识别图形是解题的关键.

练习册系列答案
相关题目
 如图,将△ABC水平向右平移了acm后,得到△A'B'C',已知BC=6cm,B C'=17cm,那么a=11cm.
如图,将△ABC水平向右平移了acm后,得到△A'B'C',已知BC=6cm,B C'=17cm,那么a=11cm.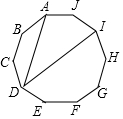 如图,在正十边形ABCDEFGHIJ中,AD、DI是两条对角线,则∠ADI=36°.
如图,在正十边形ABCDEFGHIJ中,AD、DI是两条对角线,则∠ADI=36°.