题目内容
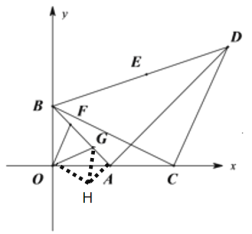
【题目】在平面直角坐标系xOy中,A(a,0),B(0,b)其中a,b满足![]() .点C为x轴正半轴上的一点,且点C在点A右侧,若点D为第一象限内一点,且满足CD⊥CB,
.点C为x轴正半轴上的一点,且点C在点A右侧,若点D为第一象限内一点,且满足CD⊥CB,![]() .
.
(1)求A,B的坐标;
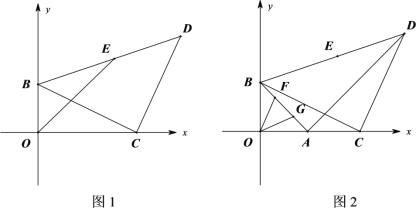
(2)如图1,点E为BD中点,连接OE,求证:![]() ;
;
(3)如图2,若点F、G是BA上的两个动点,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)证明见解析 (3)证明见解析
(2)证明见解析 (3)证明见解析
【解析】
(1)根据二次根式和平方的非负性可得![]() ,即可求出A,B的坐标;
,即可求出A,B的坐标;
(2)作![]() 与x轴交于点F,连接CE、EF,通过证明
与x轴交于点F,连接CE、EF,通过证明![]() 和
和![]() ,可得△EFO是等腰直角三角形,即可得证
,可得△EFO是等腰直角三角形,即可得证![]() ;
;
(3)将△BOF绕O点顺时针旋转90°得△AOH,旋转后点B与点A重合,点F对应点H,连接HG,根据旋转的性质得![]() ,再通过证明
,再通过证明![]() ,可得
,可得![]() ,根据勾股定理得
,根据勾股定理得![]() ,即可得证
,即可得证![]() .
.
(1)∵a,b满足![]()
∴![]()
解得![]()
∴![]() ;
;
(2)作![]() 与x轴交于点F,连接CE、EF
与x轴交于点F,连接CE、EF
∵![]() ,
,![]()
∴![]() ,△BCD是等腰直角三角形
,△BCD是等腰直角三角形
∴![]()
∵![]()
∴![]()
∴![]()
在△span>BOC和△CFD中
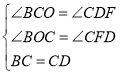
∴![]()
∴![]() ,
,![]()
∵点E为BD中点
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
在△BOE和△CFE中
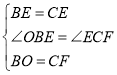
∴![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴△EFO是等腰直角三角形
∴![]() ;
;
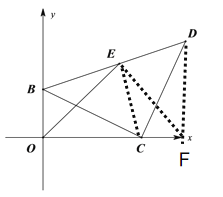
(3)将△BOF绕O点顺时针旋转90°得△AOH,旋转后点B与点A重合,点F对应点H,连接HG
根据旋转的性质得
![]() ,
,![]() ,
,![]() ,
,![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
在△FOG和△HOG中
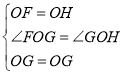
∴![]()
∴![]()
在Rt△GAH中
![]()
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.