题目内容
如图,在平面直角坐标系中,直线l: 交y轴于点A.抛物线
交y轴于点A.抛物线 的图象过点E(-1,0),并与直线l相交于A、B两点.
的图象过点E(-1,0),并与直线l相交于A、B两点.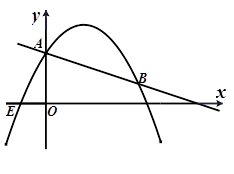
⑴ 求抛物线的解析式;
⑵ 设点P是抛物线的对称轴上的一个动点,当△PAE的周长最小时,求点P的坐标;
⑶ 在x轴上是否存在点M,使得△MAB是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
(1)抛物线的解析式是: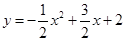
(2)P点坐标为(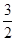 ,
,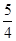 )
)
(3)在x轴上存在点M,使得△MAB是直角三角形,满足条件的点M的坐标是:M1(-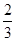 ,0),M2(
,0),M2( ,0),M3(
,0),M3(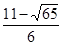 ,0),M4(
,0),M4( ,0)
,0)
解析试题分析:⑴ 直线l: 交y轴于点A(0,2),
交y轴于点A(0,2),
∵A(0,2)、E(-1,0)是抛物线 上的点,
上的点,
∴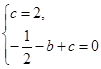 ,解得
,解得 .
.
∴抛物线的解析式是: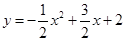 .
.
⑵ ∵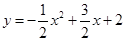 =
=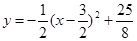 ,∴对称轴为x=
,∴对称轴为x=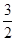 ,
,
点E(-1,0)关于x=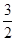 的对称点为F(4,0).
的对称点为F(4,0).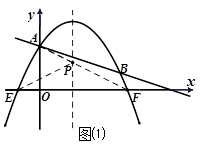
如图⑴所示,联结AF,与对称轴x=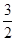 的交点即为所求P点,由于E、F两点关于对称轴对称,则此时△PAE的周长=PA+PE+AE
的交点即为所求P点,由于E、F两点关于对称轴对称,则此时△PAE的周长=PA+PE+AE
=" PA+PF+AE=" AF+AE最小.
设直线AF的解析式为y=kx+2,
把F(4,0)代入,可得4k+2=0,解得k=-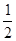 ,
,
∴直线AF解析式为y=-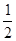 x+2.
x+2.
当x=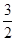 时,y=
时,y=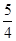 ,∴P点坐标为(
,∴P点坐标为(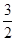 ,
,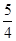 ).
).
⑶ 设在x轴上存在点M,使得△MAB是直角三角形,
① 若∠BAM=900,此时点M应在x轴的负半轴上,如图⑵,
设直线l: 交x轴于点C,令y=0,得x=6,∴C(6,0).
交x轴于点C,令y=0,得x=6,∴C(6,0).
由AM1⊥AB,OA⊥OC,可证△AOC∽△M1OA,
∴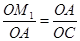 .
.
∵AO=2,OC=6,∴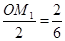 ,
,
∴OM1=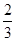 ,∴M1(-
,∴M1(-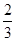 ,0).
,0).
② 若∠ABM=90°,此时点M应在x轴的正半轴上,如图⑵,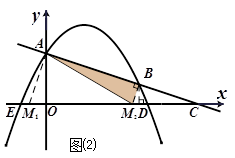
∵点B是直线 和抛物线
和抛物线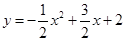 的交点,
的交点,
∴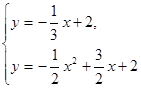 ,解得
,解得 ,或
,或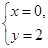 (舍)
(舍)
∴B(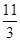 ,
,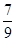 ).
).
解法一:设M(m,0),过点B作BD⊥x轴于点D,则有△BDM∽△CDB,
∴ .
.
∵BD=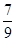 ,M2D=
,M2D=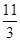 -m,CD=6-
-m,CD=6-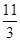 =
=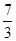 ,
,
∴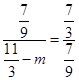 ,解得m=
,解得m= ,∴M2(
,∴M2( ,0).
,0).
解法二:过点B作BD⊥x轴于点D,
∵BM2∥AM1, ∴∠BM2D=∠AM1O,
∵tan∠AM1O= =3,
=3,
∴tan∠BM2D= =
=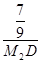 =3,
=3,
∴M2D=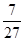 .∴OM2=OD-M2D=
.∴OM2=OD-M2D=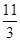 -
-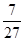 =
= ,
,
∴M2( ,0).
,0).
③ 若∠AMB=90°,则点M是以AB为直径的圆与x轴的交点,此时点M应在x轴的正半轴上,如图⑶,
设M(t,0),过点B作BD⊥x轴于点D,则有△AOM∽△MDB,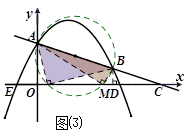
∴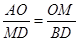 .
.
∵AO=2,MD=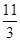 -t,OM=t,BD=
-t,OM=t,BD=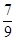 ,
,
∴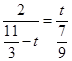 ,解得
,解得 ,
,
∴M3(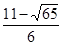 ,0),M4(
,0),M4( ,0).
,0).
综上所述,在x轴上存在点M,使得△MAB是直角三角形,满足条件的点M的坐标是:M1(-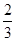 ,0),M2(
,0),M2( ,0),M3(
,0),M3(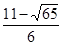 ,0),M4(
,0),M4( ,0).
,0).
考点:二次函数综合题
点评:考查函数性质与坐标关系,探究点的存在性问题,几何图形形式问题和直角三角形性质综合,中考常见压轴题目种类,难度较大。

 如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD. (2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是
(2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是 如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(4,0),D点坐标为(0,3),则AC长为
如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(4,0),D点坐标为(0,3),则AC长为 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数 ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.