题目内容
若
=
-
,则m=
5-2
|
| m |
| n |
3
3
,n=2
2
.分析:将已知的等式的左边被开方数中的5变形为2+3,根据平方根的定义将2变为(
)2,3变为(
)2,同时将2
化为2•
•
,符合完全平方公式的特点,利用完全平方公式变形后,再利用二次根式的化简公式
=|a|化简后,根据
大于
,利用绝对值的代数意义化简,与等式右边比较,即可求出m与n的值.
| 2 |
| 3 |
| 6 |
| 2 |
| 3 |
| a2 |
| 3 |
| 2 |
解答:解:∵
>
,即
-
>0,
∴
=
=
=
=|
-
|
=
-
,
又∵
=
-
,
则m=3,n=2.
故答案为:3;2
| 3 |
| 2 |
| 3 |
| 2 |
∴
5-2
|
2+3-2
|
=
(
|
=
(
|
=|
| 2 |
| 3 |
=
| 3 |
| 2 |
又∵
5-2
|
| m |
| n |
则m=3,n=2.
故答案为:3;2
点评:此题考查了二次根式的化简求值,涉及的知识有:平方根的定义,二次根式的化简公式,完全平方公式,以及绝对值的代数意义,其技巧性较强,灵活变换等式左边的被开方数是解本题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
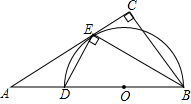 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.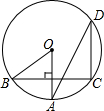 (2013•门头沟区一模)如图,OA是⊙O的半径,弦BC⊥OA,D是⊙O上一点,若∠ADC=26°,则∠AOB的度数为( )
(2013•门头沟区一模)如图,OA是⊙O的半径,弦BC⊥OA,D是⊙O上一点,若∠ADC=26°,则∠AOB的度数为( ) 如图,AB是⊙O的一条弦,CD⊥AB,垂足为C,交⊙O于点D,点E在⊙上,若∠DEB=26°,则∠OAC的度数为
如图,AB是⊙O的一条弦,CD⊥AB,垂足为C,交⊙O于点D,点E在⊙上,若∠DEB=26°,则∠OAC的度数为 如图,∠ABC=∠DBE=90°,若∠ABD=26°,则∠CBE=
如图,∠ABC=∠DBE=90°,若∠ABD=26°,则∠CBE=