Question

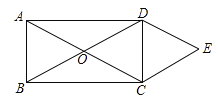
【题目】如图，已知，，，．

（1）求证：；

（2）求证：．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）根据垂直的定义和等式的基本性质可得∠EAC=∠BAF，然后利用SAS即可证出；

（2）设AB与EC的交点为O，根据全等三角形的性质可得∠AEC=∠ABF，然后根据对顶角相等可得∠AOE=∠BOM，再根据三角形的内角和定理和等量代换即可求出∠OMB=90°，最后根据垂直的定义即可证明．

解：（1）∵，，

∴∠EAB=∠CAF=90°

∴∠EAB＋∠BAC=∠CAF＋∠BAC

∴∠EAC=∠BAF

在△AEC和△ABF中

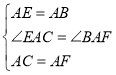
∴（SAS）

（2）设AB与EC的交点为O，如下图所示

∵

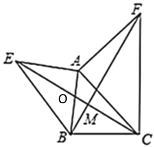
∴∠AEC=∠ABF

∵∠AOE=∠BOM

∴∠OMB=180°－∠ABF－∠BOM=180°－∠AEC－∠AOE=∠EAB=90°

∴