题目内容
设二次函数 的图象与一次函数
的图象与一次函数 的图象交于点
的图象交于点 ,若函数
,若函数 的图象与
的图象与 轴仅有一个交点,则( )
轴仅有一个交点,则( )
A.  B.
B.  C.
C.  D.
D. 
B 解析:∵ 一次函数=dx+e(d≠0)的图象经过点(),
∴ dx1+e=0, ∴ e=-dx1,∴ =d(x-).
∵ y=y2+ y 1, ∴ y =a(x- x1)(x-x2)+d(x-x1)=(x-x1).
又∵ 二次函数的图象与一次函数=dx+e(d≠0)的图象只有一个交点(),
函数y=y2+y1的图象与x轴仅有一个交点,
∴ 函数y=y2+y1是二次函数,且它的顶点是(),∴ 设y=a,
∴ (x-x1)= a.
∵ x1≠x2,∴ = a(x- x 1).
令x=x1, 则= a(x1-x1),
∴ =0,
即 .故选B.
.故选B.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
为了满足市场需求,某厂家生产A、B两种款式的环保购物袋,每天共生产5000个,两种购物袋的成本和售价如下表
| 成本(元/个) | 售价 (元/个) | |
| A | 2 | 2.4 |
| B | 3 | 3.6 |
设每天生产A种购物袋x个,每天共获利y元
(1) 求y与x的函数解析式
(2) 如果该厂每天最多投入成本12000元,那么每天最多获利多少元?
 如图,已知A(-4,n),B(2,-4)是一次函数y= k x + b的图像和反比例函数y=
如图,已知A(-4,n),B(2,-4)是一次函数y= k x + b的图像和反比例函数y= 的图像的两个交点.
的图像的两个交点.
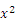 +x+c的图象与x轴有两个交点A(
+x+c的图象与x轴有两个交点A(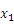 ,0),A(
,0),A(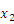 ,0),且
,0),且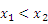 ,点P(m,n)是图象上一点,那么下列判断正确的是( )
,点P(m,n)是图象上一点,那么下列判断正确的是( )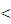 0时,m
0时,m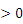 时,m>
时,m>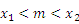 D.当n
D.当n 的图象是由函数
的图象是由函数 的图象先向 (左、右)平移
的图象先向 (左、右)平移 。机器人执行步骤是:向正前方走
。机器人执行步骤是:向正前方走 m后向左转
m后向左转 ,再依次执行相同程序,直至回到原点。现输入
,再依次执行相同程序,直至回到原点。现输入 =40,那么机器人回到原点共走了_________m.
=40,那么机器人回到原点共走了_________m.