题目内容
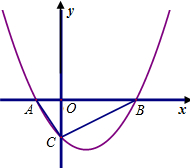
如图，AB是⊙O的直径，CD是弦，CD⊥AB于点E，
（1）求证：△ACE∽△CBE；
（2）若AB=8，设OE=x（0＜x＜4），CE2=y，请求出y关于x的函数解析式；
（3）探究：当x为何值时，tan∠D=
．
（1）求证：△ACE∽△CBE；
（2）若AB=8，设OE=x（0＜x＜4），CE2=y，请求出y关于x的函数解析式；
（3）探究：当x为何值时，tan∠D=
| ||
| 3 |
（1）证明：∵AB为⊙O直径，
∴∠ACB=90°，即∠ACE+∠BCE=90°．
又CD⊥AB，∴∠A+∠ACE=90°，
∴∠A=∠ECB，
∴Rt△ACE∽Rt△CBE；
（2）∵△ACE∽△CBE，
∴
=
，
即CE2=AE•BE=（AO+OE）（OB-OE），
∴y=（4+x）（4-x）=16-x2；
（3）∵tan∠D=
，即tan∠A=
，
∴
=
．
则
=
，
即
=
．
解得x=2或x=-4（舍去）．
故当x=2时，tan∠D=
．
∴∠ACB=90°，即∠ACE+∠BCE=90°．
又CD⊥AB，∴∠A+∠ACE=90°，
∴∠A=∠ECB，
∴Rt△ACE∽Rt△CBE；
（2）∵△ACE∽△CBE，
∴
| AE |
| CE |
| CE |
| EB |
即CE2=AE•BE=（AO+OE）（OB-OE），
∴y=（4+x）（4-x）=16-x2；
（3）∵tan∠D=
| ||
| 3 |
| ||
| 3 |
∴
| CE |
| AE |
| ||
| 3 |
则
| CE2 |
| AE2 |
| 1 |
| 3 |
即
| 16-x2 |
| (4+x)2 |
| 1 |
| 3 |
解得x=2或x=-4（舍去）．
故当x=2时，tan∠D=
| ||
| 3 |
练习册系列答案
相关题目
经过点A（1，0）和点B（0，1）．
