题目内容
已知，如图，∠AOB+∠BOC=180°，OE平分∠AOB，OF平分∠BOC．求证：OE⊥OF．考点：角平分线的定义
专题：证明题
分析：利用∠AOB+∠BOC=180°，由OE、OF分别是∠AOB和∠BOC的平分线，求出∠EOB+∠BOF=90°，即可得出结论．
解答：解：∵∠AOB+∠BOC=180°，
∵OE、OF分别是∠AOB和∠BOC的平分线，
∴∠AOE=∠EOB，∠BOF=∠FOC，
∵∠AOE+∠EOB+∠BOF+∠FOC=180°，
∴∠EOB+∠BOF=90°，
∴OE⊥OE．
∵OE、OF分别是∠AOB和∠BOC的平分线，
∴∠AOE=∠EOB，∠BOF=∠FOC，
∵∠AOE+∠EOB+∠BOF+∠FOC=180°，
∴∠EOB+∠BOF=90°，
∴OE⊥OE．
点评：本题主要考查了角平分线及垂线，解题的关键是利用角平分线求解．
练习册系列答案
全能测控一本好卷系列答案
相关题目
在△ABC中，∠B=2∠C，AD为∠A的角平分线，mAB=nBD（n＞m＞0），则cosC=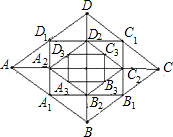
如图，以菱形ABCD各边的中点为顶点作四边形A1B1C1D1，再以A1B1C1D1各边的中点为顶点作四边形A2B2C2D2，…，如此下去，得到四边形A2013B2013C2013D22013，若ABCD对角线长分别为a和b，请用含a、b的代数式表示四边形A2013B2013C2013D2013的周长