题目内容
11. 如图,长方体的长、宽、高分别为5cm、3cm、2cm,一只蚂蚁欲从长方体底面上的点A沿着长方体表面爬到点B处,则蚂蚁需要爬行的最短路程的长为5$\sqrt{2}$cm.
如图,长方体的长、宽、高分别为5cm、3cm、2cm,一只蚂蚁欲从长方体底面上的点A沿着长方体表面爬到点B处,则蚂蚁需要爬行的最短路程的长为5$\sqrt{2}$cm.
分析 先把长方体平面展开,再根据勾股定理求解即可.
解答  解:如图1所示,
解:如图1所示,
AB=$\sqrt{(5+3)^{2}+{2}^{2}}$=2$\sqrt{17}$;
如图2所示,
AB=$\sqrt{{5}^{2}+(2+3)^{2}}$=5$\sqrt{2}$.
∵2$\sqrt{17}$>5$\sqrt{2}$,
∴它需要爬行的最短路径的长是5$\sqrt{2}$cm.
故答案为:5$\sqrt{2}$.
点评 本题考查的是平面展开-最短路径问题,熟知此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.

练习册系列答案
相关题目
1.从八边形的一个顶点出发可引出的对角线的条数有( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
19.若2axb3与-3a2by的和为单项式,则yx是( )
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
16.运用加法的运算律计算(+6$\frac{1}{3}$)+(-18)+(+4$\frac{2}{3}$)+(-6.8)+18+(-3.2)最适当的是( )
| A. | [(+6$\frac{1}{3}$)+(+4$\frac{2}{3}$)+18]+[(-18)+(-6.8)+(-3.2)] | B. | [(+6$\frac{1}{3}$)+(-6.8)+(+4$\frac{2}{3}$)]+[(-18)+18+(-3.2)] | ||
| C. | [(+6$\frac{1}{3}$)+(-18)]+[(+4$\frac{2}{3}$)+(-6.8)]+[18+(-3.2)] | D. | [(+6$\frac{1}{3}$)+(+4$\frac{2}{3}$)]+[(-18)+18]+[(-3.2)+(-6.8)] |
3.计算π0,结果是( )
| A. | 0 | B. | 1 | C. | π | D. | 3.14 |
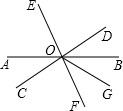 如图所示,直线AB、CD、EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=64°,求∠AOF、∠DOG的度数.
如图所示,直线AB、CD、EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=64°,求∠AOF、∠DOG的度数.