题目内容
20.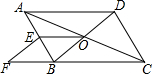 如图,在?ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD
如图,在?ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由;
(3)当线段AD和BD之间满足什么条件时,四边形OBFE是正方形?请画出图形,并说明理由.
分析 (1)证明两组对边分别平行即可.
(2)结论:当AD⊥BD时,四边形OBFE是矩形.只要证明∠BOE=90°即可.
(3)结论:当AD⊥BD AD=BD时,四边形OBFE是正方形.只要证明OB=OE即可.
解答 (1)证明:四边形ABCD是平行四边形,
∴OA=OC,
∵E为AB中点,
∴AE=BE
∴OE为△ABC的中位线,
∴OE∥BC,
∵EF∥BD,
∴四边形OBFE是平行四边形.
解:(2)结论:当AD⊥BD时,四边形OBFE是矩形
∵四边形ABCD是平行四边形,
∴OB=OD
∵E为AB中点,
∴AE=BE
∴OE为△ABD的中位线,
∴OE∥AD,
∴∠BOE=∠BDA,
∵AD⊥BD,
∴∠BOE=BDA=90°,
∵四边形OBFE是平行四边形,
∴四边形OBFE是矩形.
(3)结论:当AD⊥BD AD=BD时,四边形OBFE是正方形.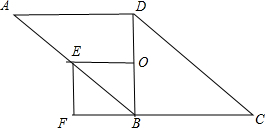
理由:∵OE为△ABD的中位线,
∴OE=$\frac{1}{2}$AD
∵O为BD中点,
∴OB=$\frac{1}{2}$BD,
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
点评 本题考查平行四边形的性质、正方形的性质和判定、矩形的判定和性质、三角形的中位线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.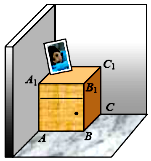 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
10.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小丽做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如由你摸球一次,你摸到白球的概率P(摸到白球)=0.6;
(3)盒子中有黑球16个.
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如由你摸球一次,你摸到白球的概率P(摸到白球)=0.6;
(3)盒子中有黑球16个.
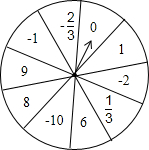 如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?
如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少? 如图,是某校三个年级学生人数分布扇形统计图,则八年级学生人数所占扇形的圆心角的度数为90°.
如图,是某校三个年级学生人数分布扇形统计图,则八年级学生人数所占扇形的圆心角的度数为90°.