题目内容
7.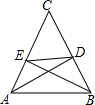 已知锐角△ABC角平分线AD与高线BE交于点M,△CDE是等边三角形,则S△DEM:S△ABM的值为( )
已知锐角△ABC角平分线AD与高线BE交于点M,△CDE是等边三角形,则S△DEM:S△ABM的值为( )| A. | $\sqrt{2}$:2 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
分析 由∠C=60°,∠BEC=90°,可得∠EBC=30°,又∠CDE=60°,∠BED=30°,可得ED=BD=CD,利用三线合一,可得AB=AC,即可得出△ABC为正三角形,AD与BE的交点为△ABC的重心,可得AM:MD=2:1,即可得出S△DEM:S△ABM的值.
解答 解:如图,
∵∠C=60°,∠BEC=90°,
∴∠EBC=30°,又∠CDE=60°,
∴∠BED=30°,
∴ED=BD=CD,
∴AD即是∠BAC的平分线,又是BC上的中线,
∴AB=AC,
∴△ABC为正三角形,
∴AD与BE的交点为△ABC的重心,
∴AM:MD=2:1,
∴S△DEM:S△ABM=1:4.
故选:D.
点评 本题主要考查了面积及等积变换,涉及等边三角形的性质,相似三角形的相似比,直角三角形的性质等知识,解题的关键是得出△ABC为正三角形.

练习册系列答案
相关题目
12.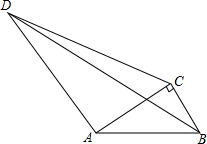 如图,Rt△ABC中,AC=2$\sqrt{3}$,∠CAB=30°,点D和点B分别在线段AC的异侧,且∠ADC=30°,连BD,则BD的最大值为2$\sqrt{7}$+2$\sqrt{3}$.
如图,Rt△ABC中,AC=2$\sqrt{3}$,∠CAB=30°,点D和点B分别在线段AC的异侧,且∠ADC=30°,连BD,则BD的最大值为2$\sqrt{7}$+2$\sqrt{3}$.
 如图,Rt△ABC中,AC=2$\sqrt{3}$,∠CAB=30°,点D和点B分别在线段AC的异侧,且∠ADC=30°,连BD,则BD的最大值为2$\sqrt{7}$+2$\sqrt{3}$.
如图,Rt△ABC中,AC=2$\sqrt{3}$,∠CAB=30°,点D和点B分别在线段AC的异侧,且∠ADC=30°,连BD,则BD的最大值为2$\sqrt{7}$+2$\sqrt{3}$.
17.甲、乙、丙三个人站在一排,通过实验可得,甲站在中间的概率为( )
| A. | $\frac{1}{6}$ | B. | $\overline{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
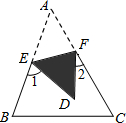 如图,△ABC中,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,求证:∠D=$\frac{1}{2}$(∠1+∠2)
如图,△ABC中,点E,F在AB,AC上,沿EF向内折叠△AEF,得△DEF,求证:∠D=$\frac{1}{2}$(∠1+∠2)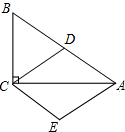 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.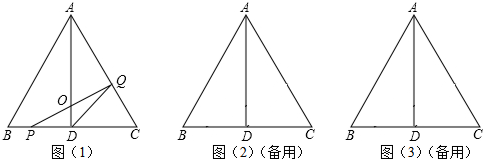
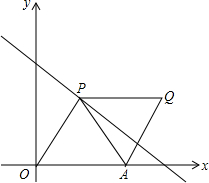 如图,点P(m,n)是直线y=-x+8上的动点,点A的坐标为(6,0),以PA为对角线,作面积为S的平行四边形OPQA.
如图,点P(m,n)是直线y=-x+8上的动点,点A的坐标为(6,0),以PA为对角线,作面积为S的平行四边形OPQA.